bugCat's Blog

毛的感情的程序猿

0%

numpy基础学习

发表于 更新于 分类于
本文字数： 9.1k 阅读时长 ≈ 8 分钟

numpy基础学习

numpy模块是学习数据分析和深度学习必须学习的内容，一个在Python中做科学计算的基础库，重在数值计算，也是大部分PYTHON科学计算库的基础库，多用于在大型、多维数组上执行数值运算，所以本篇文章主要讲解一下numpy的基础内容

官网👉https://numpy.org/

numpy创建矩阵

一般创建矩阵使用比较多的就是array、ones等函数，下面展示一些部分创建矩阵的用法

1
2
3
4
5
6
7
8
9
10
11
import numpy as np

a = np.array([1, 2, 3, 4, 5])
b = np.array(range(1, 6))
c = np.arange(1, 6)
d = np.asarray([1, 2, 3, 4, 5])

print('a', a, type(a), a.dtype)
print('b', b, type(b), b.dtype)
print('c', c, type(c), c.dtype)
print('d', d, type(d), d.dtype)

结果展示

1
2
3
4
5
D:\ProgramData\Anaconda3\python.exe E:/work_space/shixi/Problem/Test.py
a [1 2 3 4 5] <class 'numpy.ndarray'> int32
b [1 2 3 4 5] <class 'numpy.ndarray'> int32
c [1 2 3 4 5] <class 'numpy.ndarray'> int32
d [1 2 3 4 5] <class 'numpy.ndarray'> int32

上面的展示结果说明a、b、c、d内容的展示，其中a、b、c、d的内容都是1,2,3,4,5,其中a、b、c、d的类型是numpy.ndarray，其中每个元素的类型是int32

numpy中常见的数据类型

numpy常见的数据类型表展示如下

名称 描述
bool_ 布尔型数据类型（True 或者 False）
int_ 默认的整数类型（类似于 C 语言中的 long，int32 或 int64）
intc 与 C 的 int 类型一样，一般是 int32 或 int 64
intp 用于索引的整数类型（类似于 C 的 ssize_t，一般情况下仍然是 int32 或 int64）
int8 字节（-128 to 127）
int16 整数（-32768 to 32767）
int32 整数（-2147483648 to 2147483647）
int64 整数（-9223372036854775808 to 9223372036854775807）
uint8 无符号整数（0 to 255）
uint16 无符号整数（0 to 65535）
uint32 无符号整数（0 to 4294967295）
uint64 无符号整数（0 to 18446744073709551615）
float_ float64 类型的简写
float16 半精度浮点数，包括：1 个符号位，5 个指数位，10 个尾数位
float32 单精度浮点数，包括：1 个符号位，8 个指数位，23 个尾数位
float64 双精度浮点数，包括：1 个符号位，11 个指数位，52 个尾数位
complex_ complex128 类型的简写，即 128 位复数
complex64 复数，表示双 32 位浮点数（实数部分和虚数部分）
complex128 复数，表示双 64 位浮点数（实数部分和虚数部分）

数据类型的相关操作

1
2
3
4
5
6
7
8
9
import numpy as np
# 生成bool类型的
a = np.array([1, 0, 1, 0], dtype=np.bool_)
# 展示结果
print('a', a, type(a), a.dtype)
# 转化为int类型
b = a.astype(np.int8)
# 展示结果
print('b', b, type(b), b.dtype)

结果展示

1
2
3
D:\ProgramData\Anaconda3\python.exe E:/work_space/shixi/Problem/Test.py
a [ True False  True False] <class 'numpy.ndarray'> bool
b [1 0 1 0] <class 'numpy.ndarray'> int8

浮点数的相关操作

1
2
3
4
5
6
7
8
9
10
import numpy as np

# 生成均值为1.75,标准差为1的正态分布数据,10个
a = np.random.normal(1.75, 1, 10)
# 展示结果
print('a', a, type(a), a.dtype)
# 保留两位小数
b = np.round(a, 2)
# 展示结果
print('b', b, type(b), b.dtype)

结果展示

1
2
3
4
D:\ProgramData\Anaconda3\python.exe E:/work_space/shixi/Problem/Test.py
a [ 1.13844152  1.2766936   0.99489152  2.03742641  3.27012804  0.6785755
  0.39133123  0.44052134 -0.38859551  1.39006692] <class 'numpy.ndarray'> float64
b [ 1.14  1.28  0.99  2.04  3.27  0.68  0.39  0.44 -0.39  1.39] <class 'numpy.ndarray'> float64

数组的形状

numpy数组有不同的形状，有时候理解起来可能有些难以理解。特别是维度多了之后就比较晃眼，不过一般理解3维以内的就可以了。

比如这个三维数组(看有几个左括号就是几个维度)，怎么看出形状呢

1
[[[1,2,3],[1,2,3],[1,2,3]],[[1,2,3],[1,2,3],[1,2,3]]]

首先是看最里面那个[1,2,3]有三个元素，所以是3

其次是看这个[[1,2,3],[1,2,3],[1,2,3]],有三个[1,2,3]元素，所以是3

最终看[[[1,2,3],[1,2,3],[1,2,3]],[[1,2,3],[1,2,3],[1,2,3]]],有两个[[1,2,3],[1,2,3],[1,2,3]]，所以是2

综上这个数组的形状是(2,3,3)

数组形状操作

1
2
3
4
5
6
7
8
import numpy as np

a = np.array([[3, 4, 5, 6, 7, 8], [4, 5, 6, 7, 8, 9]])
print(a)
print("a的形状", a.shape)
b = a.reshape(3, 4)
print(b)
print("b的形状", b.shape)

结果展示

1
2
3
4
5
6
D:\ProgramData\Anaconda3\python.exe E:/work_space/shixi/Problem/Test.py
[[3 4 5 6 7 8]
 [4 5 6 7 8 9]]
(2, 6)
[[3 4 5 6 7 8]
 [4 5 6 7 8 9]]

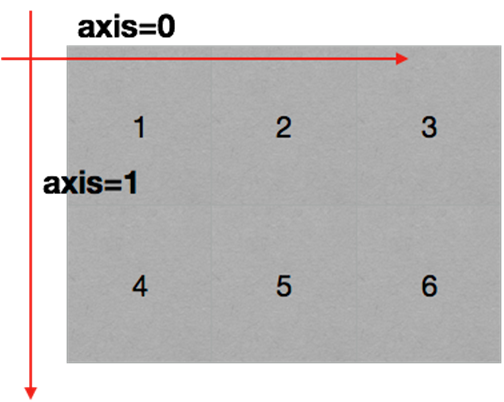
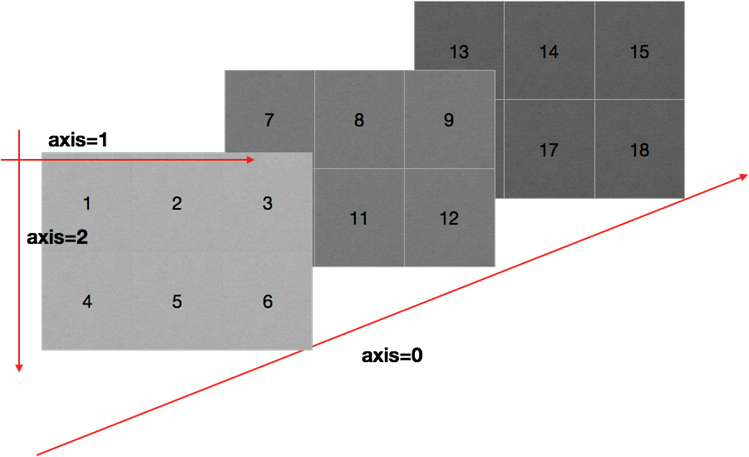
数组的轴

数组的轴在numpy中可以理解为方向,使用0,1,2…数字表示,对于一个一维数组,只有一个0轴,对于2维数组(shape(2,2)),有0轴和1轴,对于三维数组(shape(2,2, 3)),有0,1,2轴。

有了轴的概念之后,我们计算会更加方便,比如计算一个2维数组的平均值,必须指定是计算哪个方向上面的数字的平均值

如：

1
2
arr = np.random.randn(4,3)  #shape(4,3)
arr_mean = arr.mean(0)      #shape(3,)

图解：

image-20210726115552814

image-20210726115616019

数组相关的计算操作

数组和算的计算相关操作

1
2
3
4
5
6
7
8
import numpy as np

a = np.array([[3, 4, 5, 6, 7, 8], [4, 5, 6, 7, 8, 9]])
print("a的值\n", a)
b = a + 1
print("a+1的值\n", b)
c = a * 3
print("a*3的值\n", c)

结果展示如下，可以看到都是在每个位置上进行对应的操作，这个其实是numpy当中的广播机制

1
2
3
4
5
6
7
8
9
10
D:\ProgramData\Anaconda3\python.exe E:/work_space/shixi/Problem/Test.py
a的值
 [[3 4 5 6 7 8]
 [4 5 6 7 8 9]]
a+1的值
 [[ 4  5  6  7  8  9]
 [ 5  6  7  8  9 10]]
a*3的值
 [[ 9 12 15 18 21 24]
 [12 15 18 21 24 27]]

数组和数组的相关计算，数组维度相同时

1
2
3
4
5
6
7
8
9
import numpy as np

a = np.array([[3, 4, 5, 6, 7, 8], [4, 5, 6, 7, 8, 9]])
print("a的值\n", a)
b = a * 3
print("b的值\n", b)
print("a+b的值\n", a + b)
print("a-b的值\n", a - b)
print("a*b的值\n", a * b)

结果展示如下，可以看到数组相乘是对应元素的乘积，与线性代数当中的矩阵相乘不一样

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
D:\ProgramData\Anaconda3\python.exe E:/work_space/shixi/Problem/Test.py
a的值
 [[3 4 5 6 7 8]
 [4 5 6 7 8 9]]
b的值
 [[ 9 12 15 18 21 24]
 [12 15 18 21 24 27]]
a+b的值
 [[12 16 20 24 28 32]
 [16 20 24 28 32 36]]
a-b的值
 [[ -6  -8 -10 -12 -14 -16]
 [ -8 -10 -12 -14 -16 -18]]
a*b的值
 [[ 27  48  75 108 147 192]
 [ 48  75 108 147 192 243]]

数组和数组的相关计算，数组维度不同时

两个数组维度不用时，numpy当中会有一个著名的广播机制，具体的讲解可以查看https://www.cnblogs.com/jiaxin359/p/9021726.html这篇文章的讲解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import numpy as np

a = np.array([[3, 4, 5, 6, 7, 8], [4, 5, 6, 7, 8, 9]])
print("a的值\n", a)
b = np.array([1, 2, 3, 4, 5, 6])
print("b的值\n", b)
print("a+b的值\n", a + b)
print("a-b的值\n", a - b)
print("a*b的值\n", a * b)
c = np.array([[1], [2]])
print("c的值\n", c)
print("a+c的值\n", a + c)
print("a-c的值\n", a - c)
print("a*c的值\n", a * c)

结果如下，可以看到b是沿着轴0上进行广播，而c是沿着轴1上进行广播的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
D:\ProgramData\Anaconda3\python.exe E:/work_space/shixi/Problem/Test.py
a的值
 [[3 4 5 6 7 8]
 [4 5 6 7 8 9]]
b的值
 [1 2 3 4 5 6]
a+b的值
 [[ 4  6  8 10 12 14]
 [ 5  7  9 11 13 15]]
a-b的值
 [[2 2 2 2 2 2]
 [3 3 3 3 3 3]]
a*b的值
 [[ 3  8 15 24 35 48]
 [ 4 10 18 28 40 54]]
c的值
 [[1]
 [2]]
a+c的值
 [[ 4  5  6  7  8  9]
 [ 6  7  8  9 10 11]]
a-c的值
 [[2 3 4 5 6 7]
 [2 3 4 5 6 7]]
a*c的值
 [[ 3  4  5  6  7  8]
 [ 8 10 12 14 16 18]]

数组的拼接

拼接相关的函数有许多，列出下面的几个函数

函数 介绍
concatenate 提供了axis参数，用于指定拼接方向
append 默认先ravel再拼接成一维数组，也可指定axis
stack 提供了axis参数，用于生成新的维度
vstack 垂直拼接，沿着列的方向，对行进行拼接
hstack 水平拼接，沿着行的方向，对列进行拼接
dstack 沿着第三个轴（深度方向）进行拼接

concatenate

1
2
3
4
5
6
7
8
9
10
11
import numpy as np

a = np.array([[1, 2], [3, 4]])
print('数组a\n', a)
b = np.array([[5, 6]])
print('数组b\n', b)
c = np.array([[5], [6]])
print('数组c\n', b)
print('在轴0上拼接\n', np.concatenate((a, b), axis=0))
print('在轴1上拼接\n', np.concatenate((a, c), axis=1))
print('不指定轴上拼接\n', np.concatenate((a, b), axis=None))

结果展示，可以看到对于0轴和1轴上的连接是不同的，并且如果不指定轴就是变成一维

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
D:\ProgramData\Anaconda3\python.exe E:/work_space/shixi/Problem/Test.py
数组a
 [[1 2]
 [3 4]]
数组b
 [[5 6]]
数组c
 [[5 6]]
在轴0上拼接
 [[1 2]
 [3 4]
 [5 6]]
在轴1上拼接
 [[1 2 5]
 [3 4 6]]
不指定轴上拼接
 [1 2 3 4 5 6]

append

1
2
3
4
5
6
7
8
9
10
11
import numpy as np

a = np.array([[1, 2], [3, 4]])
print('数组a\n', a)
b = np.array([[5, 6]])
print('数组b\n', b)
c = np.array([[5], [6]])
print('数组c\n', b)
print('在轴0上拼接\n', np.append(a, b, axis=0))
print('在轴1上拼接\n', np.append(a, c, axis=1))
print('不指定轴上拼接\n', np.append(a, b))

结果展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
D:\ProgramData\Anaconda3\python.exe E:/work_space/shixi/Problem/Test.py
数组a
 [[1 2]
 [3 4]]
数组b
 [[5 6]]
数组c
 [[5 6]]
在轴0上拼接
 [[1 2]
 [3 4]
 [5 6]]
在轴1上拼接
 [[1 2 5]
 [3 4 6]]
不指定轴上拼接
 [1 2 3 4 5 6]

stack

stack函数比较复杂，以后再补上

vstack、hstack和dstack

vstack、hstack和dstack分别代表垂直拼接、水平拼接和深度拼接

1
2
3
4
5
6
7
8
9
import numpy as np

a = np.array((1, 2, 3))
print('数组a\n', a)
b = np.array((4, 5, 6))
print('数组b\n', b)
print('垂直拼接\n', np.vstack((a, b)))
print('水平拼接\n', np.hstack((a, b)))
print('深度拼接\n', np.dstack((a, b)))

结果展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
D:\ProgramData\Anaconda3\python.exe E:/work_space/shixi/Problem/Test.py
数组a
 [1 2 3]
数组b
 [4 5 6]
垂直拼接
 [[1 2 3]
 [4 5 6]]
水平拼接
 [1 2 3 4 5 6]
深度拼接
 [[[1 4]
  [2 5]
  [3 6]]]

可能水平和垂直比较好理解，那个深度拼接（第三个维度）就比较难以理解了，在官方文档上的解释是这等效于在形状 (M,N) 的二维阵列被重新整形为 (M,N,1) 并且形状 (N,) 的一维阵列被重新整形为 (1, N,1)。重建除以 dsplit 的数组。也就是是说二维数组和一维数组都会被重新reshape成三维数组。所以出现了上面的结果

numpy索引和切片

numpy中索引和切片和python原生的list是相同的

1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np

a = np.arange(24).reshape((4, 6))
print('展示a\n', a)
print("取一行", a[0])
print("取一列", a[:, 2])
print("取多行\n", a[0:2])
print("取多列\n", a[:, 0:2])
print("取多行多列\n", a[0:3, 0:3])
print("使用数组索引\n", a[[0, 1, 2], [0, 1, 0]])
print("使用数组索引\n", a[[0, 0, 3, 3], [0, 2, 0, 2]])
print("使用数组索引\n", a[[[0, 0], [3, 3]], [[0, 2], [0, 2]]])

结果展示，可以发现数组索引的维度会对返回后的维度产生影响

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
D:\ProgramData\Anaconda3\python.exe E:/work_space/shixi/Problem/Test.py
展示a
 [[ 0  1  2  3  4  5]
 [ 6  7  8  9 10 11]
 [12 13 14 15 16 17]
 [18 19 20 21 22 23]]
取一行 [0 1 2 3 4 5]
取一列 [ 2  8 14 20]
取多行
 [[ 0  1  2  3  4  5]
 [ 6  7  8  9 10 11]]
取多列
 [[ 0  1]
 [ 6  7]
 [12 13]
 [18 19]]
取多行多列
 [[ 0  1  2]
 [ 6  7  8]
 [12 13 14]]
使用数组索引
 [ 0  7 12]
使用数组索引
 [ 0  2 18 20]
使用数组索引
 [[ 0  2]
 [18 20]]

numpy当中还可以使用布尔索引

1
2
3
4
5
6
7
import numpy as np

a = np.arange(24).reshape((4, 6))
print('展示a\n', a)
b = a < 10
print("展示b\n", b)
print("使用布尔索引\n", a[b])

结果展示

1
2
3
4
5
6
7
8
9
10
11
12
13
D:\ProgramData\Anaconda3\python.exe E:/work_space/shixi/Problem/Test.py
展示a
 [[ 0  1  2  3  4  5]
 [ 6  7  8  9 10 11]
 [12 13 14 15 16 17]
 [18 19 20 21 22 23]]
展示b
 [[ True  True  True  True  True  True]
 [ True  True  True  True False False]
 [False False False False False False]
 [False False False False False False]]
使用布尔索引
 [0 1 2 3 4 5 6 7 8 9]

numpy中的nan和inf

nan(NAN,Nan):not a number表示不是一个数字

什么时候numpy中会出现nan？

当我们读取本地的文件为float的时候，如果有缺失，就会出现nan，或者当做了一个不合适的计算的时候(比如无穷大(inf)减去无穷大)

inf(-inf,inf):infinity,inf表示正无穷，-inf表示负无穷

什么时候回出现inf包括（-inf，+inf）？

比如一个数字除以0，（python中直接会报错，numpy中是一个inf或者-inf）

1
2
3
4
5
6
import numpy as np

a = np.inf
b = np.nan
print(type(a)) # <class 'float'>
print(type(b)) # <class 'float'>

nan需要注意的点

  1. 两个nan是不相等的

    1
    2
    np.nan==np.nan #False
    np.nan!=np.nan #True

  2. 任何值和nan进行计算都是nan

判断数组中nan的个数我们可以使用np.count_nonzero(t!=t)进行

改变数组中nan的值也可以使用t[np.isnan(t)] = 0进行

其他

numpy当中三元运算符where

1
2
3
4
5
6
7
import numpy as np

a = np.arange(10)
print('a的值\n', a)
# 将a 当中大于5的部分乘以10
print(np.where(a < 5, a, 10 * a))

结果展示

1
2
3
4
D:\ProgramData\Anaconda3\python.exe E:/work_space/shixi/Problem/Test.py
a的值
 [0 1 2 3 4 5 6 7 8 9]
[ 0  1  2  3  4 50 60 70 80 90]

numpy当中经常使用的统计函数有

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
求和：t.sum(axis=None)

均值：t.mean(a,axis=None) 受离群点的影响较大

中值：np.median(t,axis=None)

最大值：t.max(axis=None)

最小值：t.min(axis=None)

极值：np.ptp(t,axis=None) 即最大值和最小值差

标准差：t.std(axis=None)

获取最大值最小值的位置 np.argmax(t,axis=0) np.argmin(t,axis=1)

创建一个全0的数组: np.zeros((3,4))

创建一个全1的数组:np.ones((3,4))

创建一个对角线为1的正方形数组(方阵)np.eye(3)