bugCat's Blog

毛的感情的程序猿

0%

python舞蹈链数独游戏

发表于 更新于 分类于
本文字数： 9.7k 阅读时长 ≈ 9 分钟

python舞蹈链数独游戏

数独简介

数独游戏是一款古老的智力游戏，据说最早可以追溯到中国古代的“河图洛书”，但是真实可查的是在18世纪数学家欧拉等人发明了“拉丁方阵”等成为数独的最早的样子，后来经过日本的改进逐渐成为现代的数独游戏[1]。

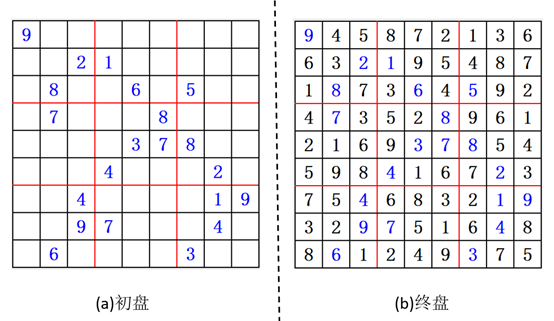
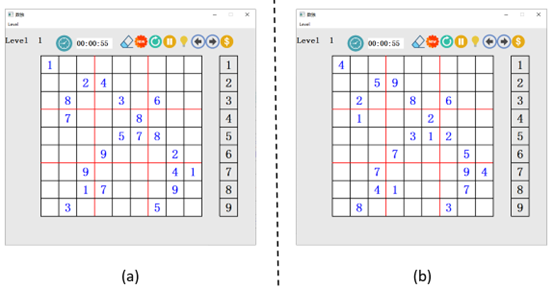
数独游戏一共有$9 \times 9$个单元格子，在数独游戏当中，玩家需要根据已有的数字去推理出所有的剩余空格的数字，并且要保证 $9 \times 9$的单位格子中每一行、每一列以及每个$3 \times 3$的九宫格内的数字不重复。数独游戏在开始的适合叫做初盘（如图1(a)所展示），包含数字和空格，当游戏成功完成时的状态叫终盘（图1(b)所展示），只有填写完成的数字。

图1

数独的解法

数独的求解方法有很有很多种，比如回溯求解、基于最小候选数求解等，本次作业我们选择的方法是基于舞蹈链的数组且介方法，在本小节会着重介绍舞蹈链以及数组求解的理论知识。

精确覆盖问题

在一个全集$X$ 中，若干子集的集合为 $S$。精确覆盖是指，$S$的子集$S^$恰好满足$X$中的每一个元素在$S^$中出现一次。这样讲可能不太通俗所以下面通过一个小例子讲解一下这个问题。

我们给定一个由0和1组成的矩阵，希望找到一个行的集合，使得集合中每一列都恰好包含一个1，矩阵如表1所示：

1 2 3 4 5 6 7
A 1 0 0 1 0 0 1
B 1 0 0 1 0 0 0
C 0 0 0 1 1 0 1
D 0 0 1 0 1 1 0
E 0 1 1 0 0 1 1
F 0 1 0 0 0 0 1

我们可以简单的通过回溯法得到最终的解是$S^*={ B,D,F}$，结果如表2所示:

1 2 3 4 5 6 7
B 1 0 0 1 0 0 0
D 0 0 1 0 1 1 0
F 0 1 0 0 0 0 1

但是在这个过程中涉及大量的矩阵进行缓存更改以及回溯的问题，这一过程是非常浪费系统资源的，所以如何优雅且高效的解决这个问题，减少系统开销，成为了算法大师们的一个问题。

舞蹈链

为了解决上面提到的回溯寻找精确覆盖问题，算法大师Donald Ervin Knuth提出了舞蹈链（Dancing Links）的数据结构，并且把求解过程称为X算法。舞蹈链的数据结构中每个节点都要6个指针，分别是：Left、Right、Up、Down、Col、Row，分别代表着左、右、上、下、行、列。舞蹈链中每一列都有特殊的结点，叫做列头，列头会记录这一列中的结点个数，列头互相连接构成了链表头，舞蹈链的图示可以参考图2。

图2

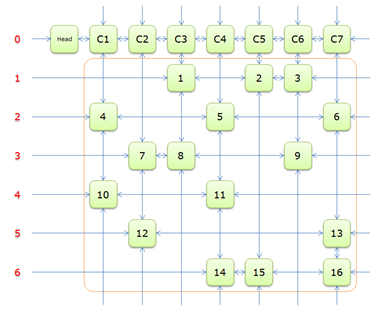
有了舞蹈链的数据结构之后，我们可以使用X算法进行求解。X算法的步骤如下：

  1. 如果矩阵$M$为空，没有任何列，则当前的选择为问题的解，返回成功；否则进入2。
  2. 选择列$c$，其中 的结点数最少的列，即1的数量最少，如果其中某一列没有1，则返回失败。
  3. 选择行$r$（其中的 $r$满足 $M_{r,c}=1$），并将 $r$加入到当前的解当中。
  4. 从矩阵$M$中删除满足 $M{r,j}=1 and M{i,j}=1$的第 $i$行和第$j$列，得到矩阵$\acute{M}$
  5. 令$M=\acute{M}$继续进入1。

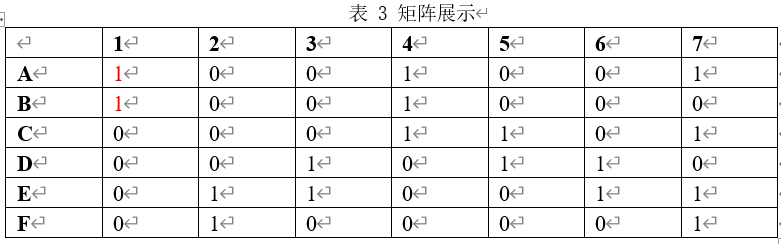
这样说可能比较抽象，让我们以表1代表的矩阵为列，进行演示：

  • 首先，因为矩阵$M$不为空，还存在列，算法没有结束。
  • 我们选择1数量最少的列“1”，如表3所展示。
1 2 3 4 5 6 7
A 1 0 0 1 0 0 1
B 1 0 0 1 0 0 0
C 0 0 0 1 1 0 1
D 0 0 1 0 1 1 0
E 0 1 1 0 0 1 1
F 0 1 0 0 0 0 1

image-20220712155430959

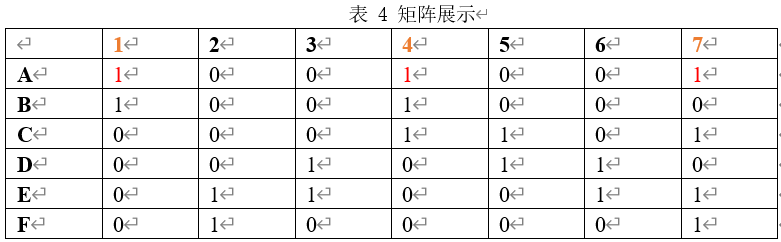
  • 因为$M{A,1}=1$并且$M{B,1}=1$所以可以依次选取 $A,B$行。
  • 先选取$A$行（将$A$行加入到当前的解中），第1、4、7列均为1，如表4所展示。
1 2 3 4 5 6 7
A 1 0 0 1 0 0 1
B 1 0 0 1 0 0 0
C 0 0 0 1 1 0 1
D 0 0 1 0 1 1 0
E 0 1 1 0 0 1 1
F 0 1 0 0 0 0 1

image-20220712155512313

  • 第1列中第$A$行和第$B$行为1，第4列中第 $A,B,C$行为1，第7列中第$A,C,E,F$行和第$1、4、7$列，如表5所展示。
1 2 3 4 5 6 7
A 1 0 0 1 0 0 1
B 1 0 0 1 0 0 0
C 0 0 0 1 1 0 1
D 0 0 1 0 1 1 0
E 0 1 1 0 0 1 1
F 0 1 0 0 0 0 1

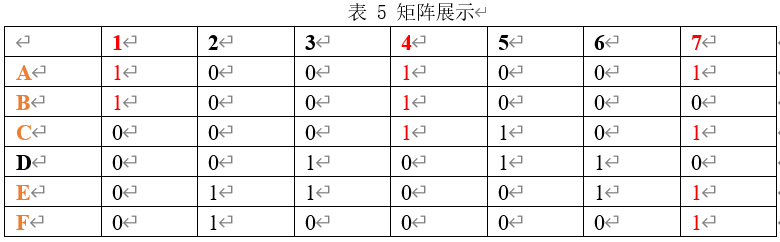
image-20220712155732882

  • 得到矩阵$\acute{M}$，继续进行递归
2 3 5 6
D 0 1 1 1

image-20220712155807311

  • 算法递归发现第2列为0，所以返回失败，所以开始选择$A$行不是算法的解，则从解中删除 $A$
  • 返回最开始的部分，将$B$行加入到当前的解中。第1、4列均为1，如表7所展示。
1 2 3 4 5 6 7
A 1 0 0 1 0 0 1
B 1 0 0 1 0 0 0
C 0 0 0 1 1 0 1
D 0 0 1 0 1 1 0
E 0 1 1 0 0 1 1
F 0 1 0 0 0 0 1

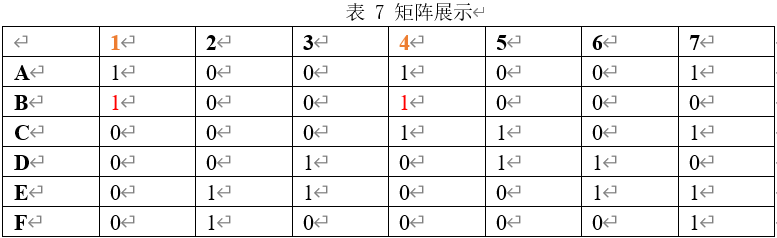
image-20220712155848091

  • 第一列中$A$行和$B$行为1，第4列中第$A,B,C$行为1。所以移除第$A,B,C$行和第1、4列，如表8所示。
1 2 3 4 5 6 7
A 1 0 0 1 0 0 1
B 1 0 0 1 0 0 0
C 0 0 0 1 1 0 1
D 0 0 1 0 1 1 0
E 0 1 1 0 0 1 1
F 0 1 0 0 0 0 1

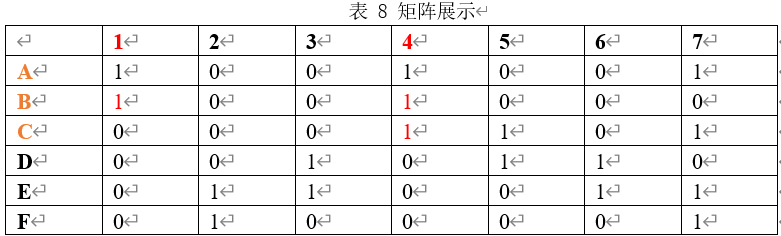
image-20220712155933356

  • 最终得到矩阵如表9所展示，并且继续进行递归
2 3 5 6 7
D 0 1 1 1 0
E 1 1 0 1 1
F 1 0 0 0 1

image-20220712160005226

  • 选择1数量最少的列“5”。
  • 将$D$行加入到当前的解中。第3、5、6列均为1。
  • 第3列中第$D、E$行为1，第5列中第$D$行为1，第6列中第$D、E$行为1。所以移除第$D、E$行和第3、5、6列。
2 3 5 6 7
D 0 1 1 1 0
E 1 1 0 1 1
F 1 0 0 0 1

image-20220712160122977

  • 最终得到矩阵如表11所展示，继续递归下去就知道这个解是成功的。
2 7
F 1 1

image-20220712160144320

  • 所以最终解为${B,D,F}$

通过这种实例展示，我们大致可以明白舞蹈链的运算过程了。这一小节如果看不太明白的可以看一下下面的链接：

https://www.cnblogs.com/grenet/p/3145800.html

https://zh.m.wikipedia.org/zh-hans/X%E7%AE%97%E6%B3%95

具体实现

整个数独游戏我采用python语言进行完成，界面采用pyqt进行编写。在这里小节介绍如何实现数组游戏，只介绍核心代码，其中几个类的关系如图所示。

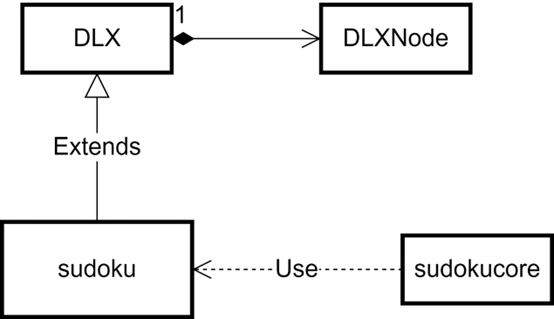
image-20220712160424299

舞蹈链实现DLX

首先是舞蹈链的结点DLXNode，我设计了主要的左、右、上、下、列头这5个指针。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 舞蹈链的结点
class DLXNode:
    def __init__(self, row=-1, col=-1):
        self.left = self
        self.right = self
        self.up = self
        self.down = self
        self.colHead = self

        # 用于列头，记录结点数
        self.count = 0
        # 单纯的标记，方便调试
        self.colId = col
        self.rowId = row

接着我开始实现DLX，DLX的数据初始时主要为一个head头节点以及一个col的数组，col数组用来存储链表头，在初始化的时候我们需要将整个head和col数组进行初始化，需要理清他们之间的指针连接，初始化输入是一个colnum，表示链表头的个数，即列的个数，可以参考下面的代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class DLX:
    def __init__(self, colnum):
        """舞蹈链初始化
        args:
            colnum:链表头个数
        """
        # self.count = 0
        # 行数
        self.rownum = 0
        # 记录行字典
        self.rowdict = {}
        self.ans = []
        self.head = DLXNode()
        self.col = [DLXNode(-1, i) for i in range(colnum)]

        # 将链表头和head连接起来
        self.head.left = self.col[-1]
        self.head.right = self.col[0]
        self.col[0].left = self.head
        self.col[0].right = self.col[1]
        self.col[-1].left = self.col[-2]
        self.col[-1].right = self.head
        # 将链表头之间连接起来
        for i in range(1, colnum-1):
            self.col[i].left = self.col[i-1]
            self.col[i].right = self.col[i+1]

DLX进行初始化之后，我们需要进行数据的插入，在这里采取的是一行一行的插入，即先插入第一行再插入第二行，所以插入的数据结点其实都是这一列最后一个结点，根据这一特点，我们进行结点上、下、左、右四个方向指针的设置，这个函数的输入是一个数组，其中元素是插入的列头id。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def pushRow(self, colList):
    """插入一行数据，按照一行一行，递增的插入
    args:
        colList:数组，里面存着列头的id
    """

    # print(colList,self.rownum)
    self.rowdict[self.rownum] = colList

    # 对于结点，列方向上，上下指针的变动
    for cowId in colList:
        # 每个插入的结点，都为该列最后一个结点
        node = DLXNode(self.rownum, cowId)
        node.down = self.col[cowId]
        node.up = self.col[cowId].up
        node.colHead = self.col[cowId]
        self.col[cowId].up.down = node
        self.col[cowId].up = node

        self.col[cowId].count += 1

    # 对于结点，行方向的两个指针的变动
    for i in range(len(colList)):
        self.col[colList[i]].up.left = self.col[colList[i-1]].up
        self.col[colList[i]].up.right = self.col[colList[(i+1) % len(colList)]].up

    self.rownum += 1

有了上面的两个函数，我们就可以创建一个DLX的数据结构了，下面就需要来进行对应结点的“跳舞”，也就是结点的删除和恢复。先介绍结点的删除，删除我采用的是给定一个列的列头，遍历列的结点进行对应的删除。需要注意的是我们删除采取的方式是改变结点a指向的结点的指针指向，但是不改变结点 的指向，这就为后续恢复结点的恢复埋下伏笔，删除函数的输入是需要删除列的列头结点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def remove(self, c: DLXNode):
    """以列为单位进行删除
    args:
        c:列头
    return:
        删除是否成功的结果
    """
    # print(c.colId,'列被删除')
    # 将列头从链表头中删除，只改变了c结点left、right的指向，并未改变c的指向，为恢复做准备
    c.left.right = c.right
    c.right.left = c.left
    if c.down == c:
        return False
    i = c.down
    while i != c:
        #遍历这一列，i为这一列中的结点
        #注意，遍历了这一列，但是并没有改变这一列结点之间的关系，为后面的恢复埋下了种子
        j = i.right
        while j != i:
            # 遍历i结点这一行，将这一行的结点进行删除
            # 注意只是改变了j结点up、down的指向，并没有改变j的指向，为后面j的恢复做准备
            j.up.down = j.down
            j.down.up = j.up
            j.colHead.count -= 1
            j = j.right
        i = i.down
    return True

结点的恢复和结点的删除刚好相反，将对应的结点添加进原始的位置，因为之前没有改变结点的指向，所以只需要根据结点自身就能进行恢复，恢复函数输入是恢复列的列头结点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def recover(self, c: DLXNode):        
    """以列为单位进行恢复
    args:
        c:列头
    return:
        恢复是否成功的结果
    """
    # print(c.colId,'列被恢复')
    i = c.down
    while i != c:
        #遍历这一列，i为这一列结点
        j = i.right
        while j != i:
            # 遍历i结点这一行，根据j结点的指向进行恢复
            j.up.down = j
            j.down.up = j
            j.colHead.count += 1
            j = j.right
        i = i.down
    # 根据c结点的指向，将c加入到链表头当中
    c.left.right = c
    c.right.left = c

接着介绍一下“跳舞”需要使用的功能寻找最少结点的列的功能，因为每个列头都记录了该列的结点数量所以只需要简单的遍历这一列就可以实现这个功能。

1
2
3
4
5
6
7
8
9
# 寻找count最小的
def FindMinCount(self):
    c = self.head.right
    minnode = c
    while c != self.head:
        if c.count < minnode.count:
            minnode = c
        c = c.right
    return minnode

有了上面的内容我们可以进行最终的“跳舞”了。过程可以简述为先选取结点数最少的列，然后将这一列的结点进行删除，然后选择其中一行作为解，然后把这一行对应的结点的列进行删除，然后进行递归最终得到解。具体的逻辑过程我们可以参考2.2节中舞蹈链的介绍。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
def Dance(self):
    # 寻找结点数最少的列
    c = self.FindMinCount()
    if c == self.head:
        return True
    
    # 删除结点数最少的列c
    if not self.remove(c):
        # print('删除失败')
        self.recover(c)
        # self.count-=1
        return False
    
    i = c.down
    while i != c:
        # 选择第i行为答案，需要将第i行上结点的列进行删除
        # print((i.rowId,i.colId),self.count)
        j = i.right
        while j != i:
            self.remove(j.colHead)
            j = j.right

        if self.Dance():
            # print("跳舞成功")
            self.ans.append(self.rowdict[i.rowId])
            return True

        # 进行回溯
        j = i.right
        while j != i:
            self.recover(j.colHead)
            j = j.right
        i = i.down

    # self.count-=1
    # 恢复被删除的列c
    self.recover(c)
    return False

数独的DLX

介绍完舞蹈链的实习之后，这一小节介绍一下如何将数独问题转化为精确覆盖问题，然后使用舞蹈链进行求解。数独规则一共有四点：

  • 每个单元格需要填写一个数字
  • 每行数字不能相同
  • 每列数字不能相同
  • 每格宫数字不能相同

我们可以把矩阵每一列都定义为一个约束，在单元格内填写数字就是加一行，然后对应的列为1，最终需要找到对应的行来覆盖这个矩阵。

针对第一条规则，我们可以使用$1-81$列进行约束，那个单元格填写了数字，那一列就会有一个结点1，假如说那个单元格没有填数字，那么第 列中某列就不会被覆盖。

针对第二条规则，我们使用$82-162$列进行约束，第82列定义成：在第1行填了数字1；……；第90列定义成：在第1行填了数字9；……；第162列定义成：在第9行填了数字9。如果第一行填写了两次1，那么矩阵中列1就会有两行，再消除的时候这两个结点会被同时消除，就会导致无法完全覆盖。

针对第三条规则，我们使用$163-243$列进行约束，第163列定义成：在第1列填了数字1；……；第171列定义成：在第1列填了数字9；……；第243列定义成：在第9列填了数字9。

针对第四条规则，我们使用$82-162$列进行约束，第244列定义成：在第1宫填了数字1；……；第252列定义成：在第1宫填了数字9；……；第324列定义成：在第9宫填了数字9。

基于上述规则，就可以把数独转化为一个精确覆盖问题的矩阵，在数独转化的时候数独有两种情况，填写了数字的单元格和没有填写数字的单元格，针对这两中情况需要分别进行处理。

有数字的单元格，我们使用$N_1,N_2,N_3,N_4$对应着规则中的列，设数字在 行 列数值为 。对应的公式如下：

其中$[]$代表取整。

对于没有数字的单元格，因为我们是进行求解，所以这个格子可能会填入$1-9$中任意一个数字，所以我们把这9个填写产生的行都插入到矩阵中，最终的解肯定是这9行之一。

代码的实现上，创建了一个sudoku类继承DLX，sudoku的初始化，函数的输入数独的数组。

1
2
3
4
5
6
7
8
9
class sudoku(DLX):
    def __init__(self, maze):
        """
        args:
            maze:大小9*9，内容为每个单元格填写的数字
        """
        super().__init__(9*9*4)
        # 切断关系采取深复制
        self.maze = copy.deepcopy(maze)

将数独转化为精确覆盖的矩阵代码实现起来不难，遍历数独数组，再按照上面介绍的进行转化就行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def pushToDLX(self):
    for x in range(9):
        for y in range(9):
            z = int(self.maze[x][y])
            colList = []
            if z != 0:
                # 单元格有数字
                N1 = x*9+y
                N2 = x*9+z+80
                N3 = y*9+z+161
                N4 = ((x//3)*3+(y//3))*9+z+242
                colList.append(N1)
                colList.append(N2)
                colList.append(N3)
                colList.append(N4)
                self.pushRow(colList)
            else:
                # 单元格没有数字，将9种可能性都插入
                for i in range(1, 10):
                    colList = []
                    z = i
                    N1 = x*9+y
                    N2 = x*9+z+80
                    N3 = y*9+z+161
                    N4 = ((x//3)*3+(y//3))*9+z+242
                    colList.append(N1)
                    colList.append(N2)
                    colList.append(N3)
                    colList.append(N4)
                    self.pushRow(colList)

最后还有一个函数就是将精确覆盖的解转化为数独数组里面的值，因为解里面存的是二维数组，一行种存的是四个列的值，可以通过一下公式进行求解。

1
2
3
4
5
6
7
8
def ans2Maze(self):
    for col in self.ans:
        x = col[0]//9
        y = col[0] % 9
        z = (col[1]-80) % 9
        if z == 0:
            z = 9
        self.maze[x][y] = z

sudokuore介绍

sudokuore是一个类用于管理数独游戏，比如什么提示、开始游戏、重新开始游戏等功能，在这里只介绍一下数组游戏中的生成数组。数组生成也有一系列的方法，比如自己随机生成一些数字填一下然后判断数字能否有解之类的，但是这种方法生成时间太长，所以我这里采取的是选一个已经生成的初盘数独，将其中数字进行变换，比如我们把初盘中“1”和“2”进行替换，那么这个数组还是一样的有解，实现了一个看起来和之前相比就是变化的，如图展示。

image-20220712162558036

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class sudokucore():
    def __init__(self):
        self.Iscanchangmaze = [[True]*9 for i in range(9)]
        self.randomList = [i for i in range(1, 10)]
        # levelfile 保存着初盘数组
        self.LevelFile = '困难.txt'
        self.initMaze()

        self.Leveldict = dict()
        self.Leveldict[1] = '简单.txt'
        self.Leveldict[2] = '普通.txt'
        self.Leveldict[3] = '困难.txt'
        print(self.Iscanchangmaze)

    def initMaze(self):

        self.maze = []
        with open(self.LevelFile, 'r') as f:
            for line in f.readlines():
                self.maze.append(line.strip().split(','))
        # 进行洗牌
        random.shuffle(self.randomList)
        print(self.randomList)
        self.colDict = {}
        for i in range(9):
            self.colDict[self.randomList[i]] = i
        # 进行变换
        print(self.colDict)
        for i in range(9):
            for j in range(9):
                z = int(self.maze[i][j])
                if z != 0:
                    index = self.colDict[z]
                    # 对应的数字进行变换
                    self.maze[i][j] = self.randomList[(index+1) % 9]
                    self.Iscanchangmaze[i][j] = False

运行结果展示

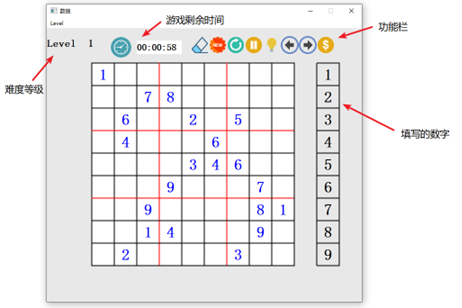
界面运行和各个部分的功能展示，如图5所展示

图5

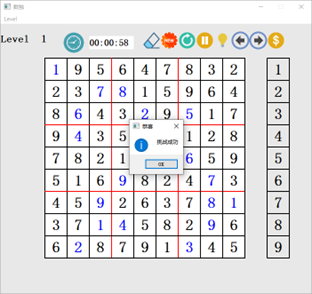
全部填写完成后结果展示如图6所示

图6

总结

这次的数独小游戏，让我学习到了如何完成一个完整的小工程，也学习了舞蹈链的编写和实现，这个项目还有许多值得改进的地方，希望后续有时间再进行改进吧。

仓库地址：https://github.com/bugcat9/sudoku

参考：