深入理解计算机系统第2章练习题

练习题2.1完成下面的数字转换:

A.将0x39A7F8转换为二进制。

$$(39A7F8)_{16} = (0011-1001-1010-0111-1111-1000)_2$$

B.将二进制1100100101111011转换为十六进制。

$$(1100-1001-0111-1011)_2 = (C97B)_{16}$$

C.将0xD5E4C转换为二进制。

$$(D5E4C)_{16} = (1101-0101-1110-0100-1100)_2$$

D.将二进制1001101110011110110101转换为十六进制。

$$(10-0110-1110-0111-1011-0101)_2 =(26E7B5)_{16}$$

练习题2.2 填写下表中的空白项,给出2的不同次幂的二进制和十六进制表示‥

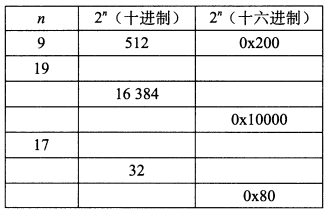
$n$	$2^n$(十进制)	$2^n$(十六进制)
9	512	0x200
19	524288	0x80000
14	16384	0x4000
16	65536	0x10000
17	131072	0x20000
5	32	20
7	128	0x80

练习题2.3 一个字节可以用两个十六进制数字来表示。填写下表中缺失的项,给出 不同字节模式的十进制、二进制和十六进制值:

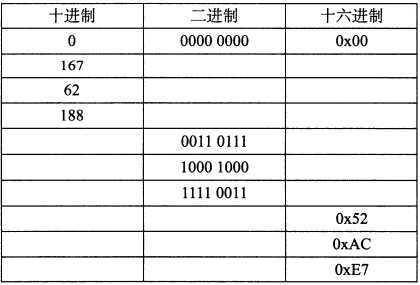
十进制	二进制	十六进制
0	0000 0000	0x00
167	1010 0111	0xA7
62	0011 1110	0x3E
188	1011 1100	0xBC
55	0011 0111	0x37
136	1000 1000	0x88
243	1111 0011	0xF3
82	0101 0010	0x52
172	1010 1100	0xAC
231	1110 0111	0xE7

练习题2.4 不将数字转换为十进制或者二进制,试着解答下面的算术题,答案要用 十六进制表示。提示:只要将执行十进制加法和减法所使用的方法改成以16为基数。

A. 0x503C + 0x8

0x503C + 0x8 = 0x5044

B. 0x503C - 0x40

0x503C - 0x40 = 0x4F9C

C. 0x503C + 64

0x503C + 64 = 0x507c

D. 0x50EA - 0x503C

0x50EA - 0x503C = 0xAF

练习题2.5 思考下面对show上ytes的三次调用:

#include <stdio.h>

typedef unsigned char *byte_pointer;

void show_bytes(byte_pointer start, size_t len)
{
    size_t i;
    for (i = 0; i < len; i++)

        printf(" %.2x", start[i]);

    printf("\n");
}

void show_int(int x)
{
    show_bytes((byte_pointer)&x, sizeof(int));
}

void show_float(float x)
{
    show_bytes((byte_pointer)&x, sizeof(float));
}

void show_pointer(void *x)
{
    show_bytes((byte_pointer)&x, sizeof(void *));
}

int val = 0x87654321;
byte_pointer valp = (byte_pointer) &val;
show_bytes(valp, 1);    // A.
show_bytes(valp, 2);    // B.
show_bytes(valp, 3);    // C.

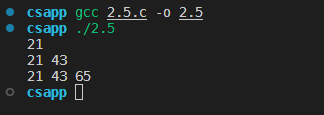
指出在小端法机器和大端法机器上,每次调用的输出值。

在小端机上调用了一下，大端机只能使用模拟器目前不打算调用。

练习题2.6 使用show_int和show_float,我们确定整数3510593的十六进制表示为0x00359141,而浮点数3510593.0的十六进制表示为0x4A564504。

A.写出这两个十六进制值的二进制表示

0x00359141 0000 0000 0011 0101 1001 0001 0100 0001

0x4A564504 0100 1010 0101 0110 0100 0101 0000 0100

B.移动这两个二进制串的相对位置,使得它们相匹配的位数最多。有多少位相匹配呢?

可以看到移动两位后，最多11位相匹配。

C.串中的什么部分不相匹配?

这个跟浮点数的存储有关，后续应该会学习到。

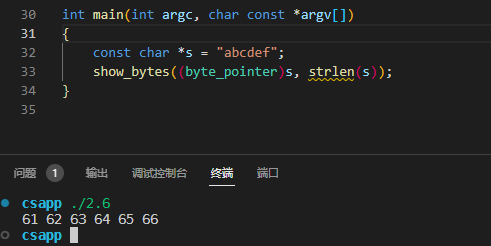
练习题2.7 下面对show_bytes的调用将输出什么结果?

const char *s = "abcdef";
show_bytes((byte_pointer)s,strlen(s));

注意字母a~z的ASCII码为 0x61~0x7A

练习题2.8 填写下表,给出位向量的布尔运算的求值结果。

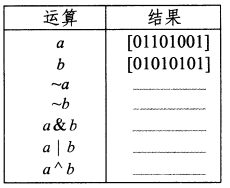
运算	结果
a	[01101001]
b	[01010101]
~a	[10010110]
~b	[10101010]
a&b	[01000001]
a\	b	[01111101]
a^b	[00111100]

练习题2.9

通过混合三种不同颜色的光(红色、绿色和蓝色),计算机可以在视频屏 幕或者液晶显示器上产生彩色的画面。设想一种简单的方法,使用三种不同颜色的 光,每种光都能打开或关闭,投射到玻璃屏幕上,如图所示:

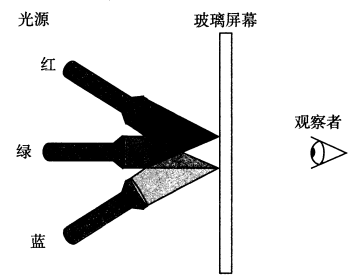
那么基于光源R(红)、 G(绿)、 B(蓝)的关闭(0)或打开(1),我们就能够创建8 种不同的颜色:

这些颜色中的每一种都能用一个长度为3的位向量来表示,我们可以对它们进行布尔运算。

A.一种颜色的补是通过关掉打开的光源,且打开关闭的光源而形成的。那么上面列 出的8种颜色每一种的补是什么?

原颜色	代码	补码	补颜色
黑色	000	111	白色
蓝色	001	110	黄色
绿色	010	101	红绿色
蓝绿色	011	100	红色
红色	100	111	蓝绿色
红紫色	101	010	绿色
黄色	110	001	蓝色
白色	111	000	黑色

B.描述下列颜色应用布尔运算的结果:

蓝色 | 绿色 = (001 | 010) = 011 = 蓝绿色

黄色 & 蓝绿色 = (110 & 011) = 010 = 绿色

红色 ^ 红紫色 = (100 ^ 101) = 001 = 蓝色

练习题2.10 对于任一位向量a,有a^a=0应用这一属性,考虑下面的程序:

void inplace_swap(int *x, int *y)
{
    *y = *x ^ *y; /* Step 1 */
    *x = *x ^ *y; /* Step 2 */
    *y = *x ^ *y; /* Step 3 */
}

正如程序名字所暗示的那样,我们认为这个过程的效果是交换指针变量x和y所指向 的存储位置处存放的值。注意,与通常的交换两个数值的技术不一样,当移动一个值 时,我们不需要第三个位置来临时存储另一个值。这种交换方式并没有性能上的优 势,它仅仅是一个智力游残。

以指针x和y指向的位置存储的值分别是α和6作为开始,填写下表,给出在程序的 每一步之后,存储在这两个位置中的值。利用^的属性证明达到了所希望的效果。回 想一下,每个元素就是它自身的加法逆元(a^a=0)。

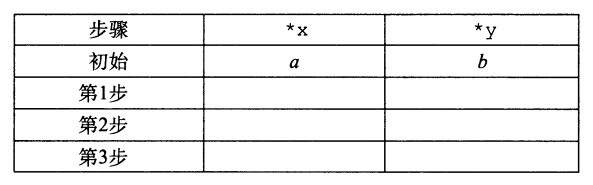
步骤	*x	*y
初始	a	b
第1步	a	a^b
第2步	a\^a\^b=b	a^b
第3步	b	b\^a\^b=a

练习题2.11在练习题2.10中的inplace_swap函数的基础上,你决定写一段代码, 实现将一个数组中的元素头尾两端依次对调。你写出下面这个函数:

void reverse_array(int a[], int cnt)
{
    int first, last;
    for (first = 0, last = cnt - 1; first <= last; first++, last--)
    {
        inplace_swap(&a[first], &a[last]);
    }
}

当你对一个包含元素1、 2、 3和4的数纽使用这个函数时,正如预期的那样,现在数 纽的元素变成了4、3、2和1。不过,当你对一个包含元素1、2、3、4和5的数纽使 用这个函数时,你会很惊奇地看到得到数字的元素为5、 4、0、 2和1。实际上,你会 发现这段代码对所有偶数长度的数组都能正确地工作,但是当数组的长度为奇数时, 它就会把中间的元素设置成0。

A.对于一个长度为奇数的数纽,长度cnt=2k+1,函数reverse_array最后一次循环中,变量first和Iast的值分别是什么?

最后一次循环时，变量first = a[k]，last = a[k]。

B.为什么这时调用函数inplace_swap会将数组元素设置为0?

因为最后一次循环时，变量first = a[k]，last = a[k]。他们之间进行inplace_swap

第一步 y = x ^ *y; 替换之后a[k] = a[k] ^ a[k] =0;

第二步x = x ^ *y; 替换之后a[k] = 0 ^ 0 =0;

第二步y = x ^ *y; 替换之后a[k] = 0 ^ 0 =0;

C.对reverse_array的代码做哪些筒单改动就能消除这个问题?

只需要将first <= last改为first < last即可

练习题2.12 对于下面的值,写出变量x的C语言表达式。

你的代码应该对任何字 长$w\geq8$都能工作。我们给出了当x=0x87654321以及$w=32$时表达式求值的结果, 仅供参考。

A. x的最低有效字节,其他位均置为0。[0x00000021]。

x & 0xFF

B.除了x的最低有效字节外,其他的位都取补,最低有效字节保持不变。 [0x789ABC21]。

~(x ^ 0xFF)或者x ^ (~0xFF)

C.x的最低有效字节设置成全1，其他字节都保持不变。[0x876543FF]。

x | 0xFF

练习题2.13

从20世纪70年代末到80年代末，Digital Equipment的 VAX计算机是一种非常流行的机型。它没有布尔运算AND 和OR指令，只有bis(位设置)和bic(位清除)这两种指令。两种指令的输入都是一个数据字x和一个掩码字m。它们生成一个结果z，z是由根据掩码m的位来修改x的位得到的。使用bis 指令，这种修改就是在m为1的每个位置上，将z对应的位设置为1。使用bic指令，这种修改就是在m为1的每个位置，将z对应的位设置为0。

为了看清楚这些运算与C语言位级运算的关系，假设我们有两个函数bis和 bic来实现位设置和位清除操作。只想用这两个函数，而不使用任何其他C语言运算，来实现按位|和~运算。填写下列代码中缺失的代码。提示:写出bis和 bic运算的C语言表达式。

int bis(int x, int m);
int bic(int x, int m);

int bool_or(int x, int y)
{
    int result = bis(x, y);
    return result;
}

int bool_xor(int x, int y)
{
    int result = bis(bic(x, y), bic(y, x));
    return result;
}

练习题2.14 假设x和y的字节值分别为0x66和0x39。填写下表，指明各个C表达式的字节值。

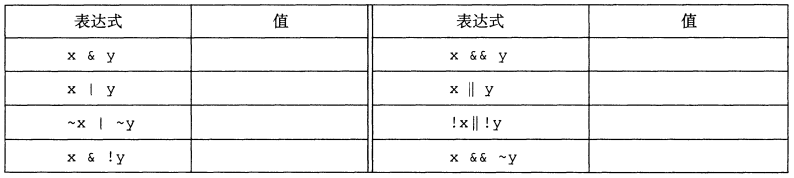
0x66 = 0110 0110

0x39 = 0011 1001

表达式	值
x & y	0110 0110 & 0011 1001 = 0010 0000 = 0x20
x \	y	0110 0110 \	0011 1001 = 0111 1111 = 0x7F
~x \	~y	~0110 0110 \	~0011 1001 = 1001 1001 \	1100 0110 = 1101 1111 = 0xDF
x & !y	0110 0110 & !0011 1001 = 0110 0110 & 0000 0000 = 0x00
x && y	0x01
x \	\	y	0x01
!x \	\	!y	0x00
x && ~y	0x01

练习题2.15︰只使用位级和逻辑运算，编写一个C表达式，它等价于x= =y。换句云说，当x和y相等时它将返回1，否则就返回0。

!(x^y)

练习题2.16

填写下表，展示不同移位运算对单字节数的影响。思考移位运算的最好方式是使用二进制表示。将最初的值转换为二进制，执行移位运算，然后再转换回十六进制。每个答案都应该是8个二进制数字或者2个十六进制数字。

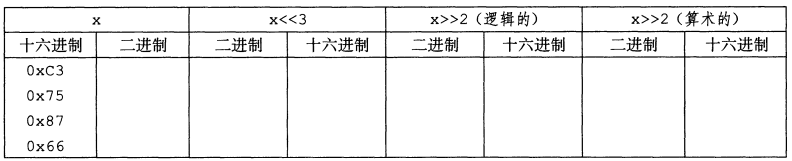
x		x<<3		x>>2(逻辑)		x>>2(算术)
十六进制	二进制	二进制	十六进制	二进制	十六进制	二进制	十六进制
0xC3	1100 0011	0001 1000	0x18	0011 0000	0x30	1111 0000	0xF0
0x75	0111 0101	1010 1000	0xA8	0001 1101	0x1D	0001 1101	0x1D
0x87	1000 0111	0011 1000	0x38	0010 0001	0x21	1110 0001	0xE1
0x66	0110 0110	0011 0000	0x30	0001 1001	0x19	0001 1001	0x19

练习题2.17

假设w=4（字长为4），我们能给每个可能的十六进制数字赋予一个数值，假设用一个无符号或者补码表示。请根据这些表示，通过写出等式(2.1)和等式(2.3)所示的求和公式中的2的非零次幂，填写下表:

x		无符号(B2U(x))	补码(B2T(x))
十六进制	二进制
0xE	1110	14	-2
0x0	0000	0	0
0x5	0101	5	5
0x8	1000	8	-8
0xD	1101	13	-3
0xF	1111	15	-1

练习题2.18

在第3章中，我们将看到由反汇编器生成的列表，反汇编器是一种将可执行程序文件转换回可读性更好的ASCII码形式的程序。这些文件包含许多十六进制数字，都是用典型的补码形式来表示这些值。能够认识这些数字并理解它们的意义(例如它们是正数还是负数)，是一项重要的技巧。

在下面的列表中，对于标号为A～I(标记在右边)的那些行，将指令名(sub、mov和add)右边显示的(32位补码形式表示的)十六进制值转换为等价的十进制值。

32位补码	十进制
0x2e0	736
0x58	88
0x28	40
0x30	48
0x78	120
0x88	136
0x1f8	504
0x8	8
0xc0	192
0x48	72

练习题2.19 利用你解答练习题2.17时填写的表格，填写下列描述函数T2U。的表格。

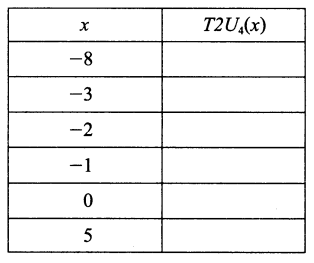
x	T2U(x)
-8	8
-3	13
-2	14
-1	15
0	0
5	5

练习题2.20

请说明等式(2.5)是如何应用到解答练习题2.19时生成的表格中的各项的。反过来看，我们希望推导出一个无符号数$u$和与之对应的有符号数$U2T_w(u)$之间的关系:

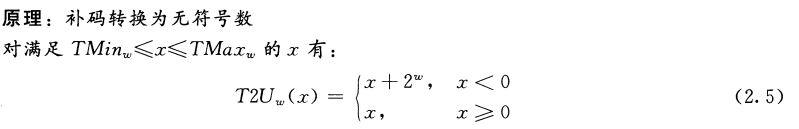
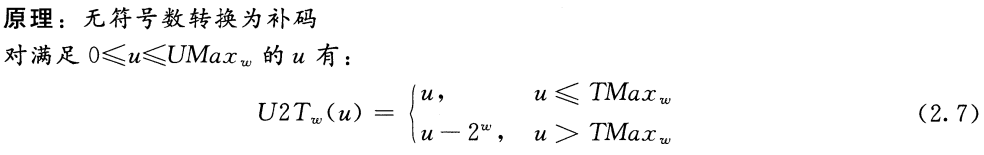
练习题2.21 假设在采用补码运算的32位机器上对这些表达式求值，按照图2-19的格式填写下表，描述强制类型转换和关系运算的结果。

表达式	类型	求值
-2147483647-1==2147483648U	无符号	1
-2147483647-1<2147482647	有符号	1
-2147483647-1U < 2147483647	无符号	0
-2147483647-1<-2147482647	有符号	1
-2147483647-1U<-2147482647	无符号	1

练习题2.22 通过应用等式(2.3)，表明下面每个位向量都是-5的补码表示。

A.[1011]

1011 = -2^3+2+1 = -5

B.[11011]

11011 = -2\^4+2\^3+2+1 = -5

C.[111011]

111011 = -2\^5+2\^4+2\^3+2+1 = -5

练习题2.23考虑下面的C函数

int funl(unsigned word)
{
    return (int)((word << 24) >> 24);
}

int fun2(unsigned word)
{
    return ((int)word << 24) >> 24;
}

假设在一个采用补码运算的机器上以32位程序来执行这些函数。还假设有符号数值的右移是算术右移，而无符号数值的右移是逻辑右移。

A.填写下表，说明这些函数对几个示例参数的结果。你会发现用十六进制表示来做会更方便，只要记住十六进制数字8到F的最高有效位等于1。

写下如下代码

#include "stdio.h"

int fun1(unsigned word)
{
    return (int)((word << 24) >> 24);
}

int fun2(unsigned word)
{
    return ((int)(word << 24)) >> 24;
}

int main()
{
    unsigned int a1 = 0x00000076;
    unsigned int a2 = 0x87654321;
    unsigned int a3 = 0x000000C9;
    unsigned int a4 = 0xEDCBA987;
    printf("fun1(a1) %x,", fun1(a1));
    printf("fun2(a1) %x\n", fun2(a1));

    printf("fun1(a2) %x,", fun1(a2));
    printf("fun2(a2) %x\n", fun2(a2));

    printf("fun1(a3) %x,", fun1(a3));
    printf("fun2(a3) %x\n", fun2(a3));

    printf("fun1(a4) %x,", fun1(a4));
    printf("fun2(a4) %x\n", fun2(a4));
}

w	fun1(w)	fun2(w)
0x00000076	0x00000076	0x00000076
0x87654321	0x00000021	0x00000021
0x000000c9	0x000000C9	0xffffffC9
0xEDCBA987	0x00000087	0xffffff87

B.用语言来描述这些函数执行的有用的计算。

练习题2.24 假设将一个4位数值(用十六进制数字0～F表示)截断到一个3位数(用十六进制数字0～7表示)。填写下表，根据那些位模式的无符号和补码解释，明这种截断对某些情况的结果。

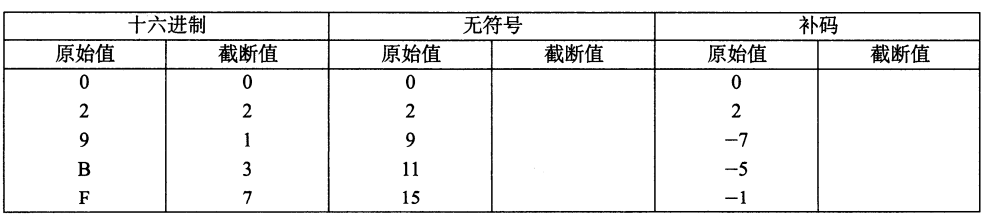
解释如何将等式(2.9)和等式(2.10)应用到这些示例上。

十六进制		无符号		补码
原始值	截断值	原始值	截断值	原始值	截断值
0	0	0	0	0	0
2	2	2	2	2	2
9	1	9	1	-7	1
B	3	11	3	-5	3
F	7	15	7	-1	-1

练习题2.25考虑下列代码，这段代码试图计算数组a中所有元素的和，其中元素的数量由参数length 给出。

float sum_elements(float a[], unsigned length)
{
    int i;
    float result = 0;
    for (i = 0; i <= length - 1; i++)
    {
        result += a[i];
    }

    return result;
}

当参数length等于0时，运行这段代码应该返回0.0。但实际上，运行时会遇到一个内存错误。请解释为什么会发生这样的情况，并且说明如何修改代码。

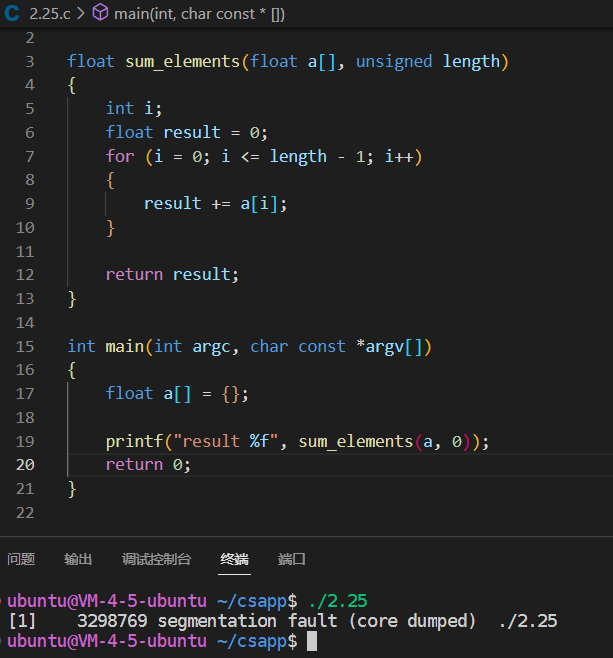
原因是length的类型是unsigned 但是1的类型是是int，所以计算转为无符号数计算，length - 1=length +（- 1），现在的问题是-1的无符号数是多少-1的十六进制无符号数为0xFFFFFFFF换算之后是4294967295,所以代码就出现了异常,for循环进去之后数组下标越界。只需要将unsigned 改为int即可。

练习题2.26现在给你一个任务，写一个函数用来判定一个字符串是否比另一个更长。前提是你要用字符串库函数strlen，它的声明如下:

#include "stdio.h"

size_t strlen(const char *s);

int strlonger(char *s, char *t)
{
    return strlen(s) - strlen(t) > 0;
}

当你在一些示例上测试这个函数时，一切似乎都是正确的。进一步研究发现在头文件stdio.h中数据类型size_t是定义成unsigned int的。

A.在什么情况下，这个函数会产生不正确的结果？

当s字符串的长度strlen1小于t字符串的长度strlen2时。

B.解释为什么会出现这样不正确的结果?

当s字符串的长度strlen1小于t字符串的长度strlen2时，strlen1-strlen2应当是负数，但是size_t是无符号，根据无符号数的方式解释器补码，这个负数是一个很大的正数。然后正数是大于0，不等式成立，函数就会返回逻辑True。

C.说明如何修改这段代码好让它能可靠地工作。

修改后的表达式：return strlen(s)>strlen(t);

练习题2.27 写出一个具有如下原型的函数:

int uadd_ok(unsigned x,unsigned y) 

如果参数x和y相加不会产生溢出，这个函数就返回1。

int uadd_ok(unsigned x,unsigned y) {
    unsigned result = x + y;
    return result >= x;
}

练习题2.28我们能用一个十六进制数字来表示长度w=4的位模式。对于这些数字的无符号解释，使用等式(2.12)填写下表，给出所示数字的无符号加法逆元的位表示(用十六进制形式)。

$x$		$-^u_4x$
十六进制	十进制	十六进制	十进制
0	0	0	0
5	5	B	11
8	8	8	8
D	13	3	3
F	15	1	1

练习题2.29按照图2-25的形式填写下表。分别列出5位参数的整数值、整数和与补码和的数值、补码和的位级表示，以及属于等式(2.13)推导中的哪种情况。

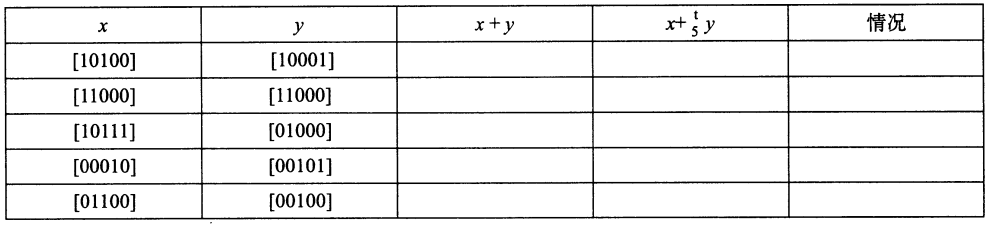
$x$	$y$	$x+y$	$x+^t_5y$	情况
[10100] -12	[10001] -15	[100101] -27	[00101] 5	1
[11000] -8	[11000] -8	[110000] -16	[10000] -16	2
[10111] -9	[01000] 8	[11111] -1	[11111] -1	2
[00010] 2	[00101] 5	[00111] 7	[00111] 7	3
[01100] 12	[00100] 4	[10000] 16	[10000] -16	-16

练习题2.30写出一个具有如下原型的函数:

/* Determine whether arguments can be added without overflow */
int tadd_ok(int x, int y);

如果参数x和y相加不会产生溢出，这个函数就返回1。

int tadd_ok(int x, int y)
{
    int s = x + y;
    if (x > 0 && y > 0)
        return s > 0;

    if (x < 0 && y < 0)
        return s < 0;

    return 1;
}

练习题2.31你的同事对你补码加法溢出条件的分析有些不耐烦了，他给出了一个函数tadd_ok的实现，如下所示:

// determin whether arguments can be added without overflow
// WARNING: THIS code is buggy
int tadd_ok(int x, int y)
{
    int sum = x + y;
    return (sum - x == y) && (sum - y == x);
}

你看了代码以后笑了。解释一下为什么。

因为sum-x与y是恒相等的。

假设int的w是4，即字长为4，并且sum=x+y发生正溢出（x>0,y>0,sum<=0）。那么sum = x+y-16。

sum-x = x+y-16-x = y-16。因为字长是4，并且y>0 ，所以y = y-16是恒等的。也就是说sum-x=y是永远成立的。

同理可以得出负溢出的情况。所以就算一簇上述代码也不会返回0，代码是错误的。

练习题2.32你现在有个任务，编写函数tsub_ok 的代码，函数的参数是x和y，如果计算x-y不产生溢出，函数就返回1。假设你写的练习题2.30的代码如下所示:

int tsub_ok(int x, int y)
{
    return tadd_ok(x, -y);
}

x和y取什么值时，这个函数会产生错误的结果?写一个该函数的正确版本(家庭作业2.74)。

当y = INT_MIN时会发生错误。

在计算机当中，y = INT_MIN时，-y = INT_MIN（会发生溢出）。所以这时tadd_ok(x, -y)会判断错误。

至于正确答案，如果-y = INT_MIN理解为也算溢出的话，答案应该如下

int tsub_ok(int x, int y)
{
    if (y == INT_MIN) //只要y为INT_MIN，就直接返回0
        return 0;
    return tadd_ok(x, -y);
}

练习题2.33我们可以用一个十六进制数字来表示长度w=4的位模式。根据这些数字的补码的解释，填写下表，确定所示数字的加法逆元。

对于补码和无符号(练习题2.28)非(negation)产生的位模式，你观察到什么?

$x$		$-^t_4x$
十六进制	十进制	十六进制	十进制
0	0	0	0
5	5	B	-5
8	-8	8	-8
D	-3	3	3
F	-1	1	1

练习题2.34 按照图2-27的风格填写下表，说明不同的3位数字乘法的结果。

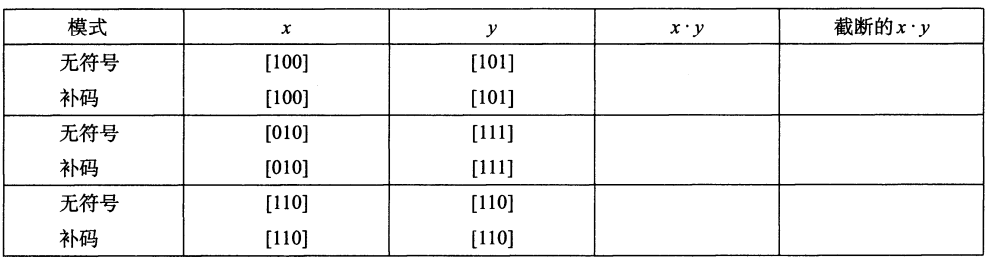
模式	x	y	x*y	截断的x*y
无符号	[100] 4	[101] 5	[001 0100] 20	[100] 4
补码	[100] -4	[101] -3	[000 1100] 12	[100] -4
无符号	[010] 2	[111] 7	[000 1110] 14	[110] 6
补码	[010] 2	[111] -1	[111 1110] -2	[110] -2
无符号	[110] 6	[110] 6	[010 0100] 36	[100] 4
补码	[110] -2	[110] -2	[000 0100 ] 4	[100] -4

练习题2.35﹐ 给你一个任务，开发函数tmult ok 的代码，该函数会判断两个参数相乘是否会产生溢出。下面是你的解决方案:

/* Determine whether arguments can be multiplied without overflow */
int tmult_ok(int x, int y)
{
    int p = x * y;
    /*Either x is zero, or dividing p by x gives y */
    return !x || p / x == y;
}

练习题2.36对于数据类型int为32位的情况，设计一个版本的tmult_ok函数(练习题2.35)，使用64位精度的数据类型int64_t，而不使用除法。

int tmult_ok2(int32_t x, int32_t y)
{
	int64_t p = (int64_t)x * y; /*一定要先将右边手动转成 int64_t */
	/*printf("p=%" PRId64 ", q=%" PRId32 "\n", p,q);*/

	return p == (int32_t)p;
}

练习题2.37现在你有一个任务，当数据类型int和size_t 都是32位的，修补上述旁注给出的XDR代码中的漏洞。你决定将待分配字节数设置为数据类型uint64_t，来消除乘法溢出的可能性。你把原来对malloc函数的调用(第9行)替换如下:

uint64_t asize = ele_cnt * (uint64_t) ele_size;
void *result = malloc(asize);

提醒一下，malloc 的参数类型是size_t。

A．这段代码对原始的代码有了哪些改进?

假设会溢出，那么虽然到了asize这步还不会溢出，因为在等式右边已经先把两个乘子强制类型转换为uint64_t了。
但是到了malloc函数时，由于此函数的原型设计，还是会被截断，传入malloc函数时发生溢出。

B.你该如何修改代码来消除这个漏洞?

练习题2.38就像我们将在第3章中看到的那样，LEA指令能够执行形如(a<<k)+b的计算，这里k 等于0、1、2或3，而b等于0或者某个程序值。编译器常常用这条指令来执行常数因子乘法。例如，我们可以用(a<<1)+a来计算3*a。考虑b等于0或者等于a、k为任意可能的值的情况，用一条LEA指令可以计算a的哪些倍数?

当b=0时，(a<<k)+b = a*2\^k，而k=0、1、2或3，所以结果为a，2a，4a，8a

当b=a时，(a<<k)+a = a(2^k+1)，而k=0、1、2或3，所以结果为2a，3a，5a，9a

综上：结果为a，2a，3a，4a，5a，8a，9a

练习题2.39对于位位置n为最高有效位的情况，我们要怎样修改形式B的表达式?

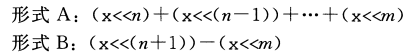
这个表达式就变成了$-(x<<m)$。要看清这一点，设字长为$w$，$n=w—1$。形式B说我们要计算$(x<<w)-(x<<m)$，但是将x向左移动w位会得到值0。

练习题2.40对于下面每个K的值，找出只用指定数量的运算表达x* K 的方法﹐这里我们认为加法和减法的开销相当。除了我们已经考虑过的简单的形式A和B原则,你可能会需要使用一些技巧。

K	移位	加法/减法	表达式
6	2	1	(x << 2) + (x<<1)
31	1	1	(x <<5 ) - x
-6	2	1	(x << 1) - (x << 3)
55	2	2	(x << 6) - (x <<3) - x

练习题2.41对于一组从位位置n开始到位位置m 的连续的1(n≥m)，我们看到可以产生两种形式的代码，A和B。编译器该如何决定使用哪一种呢?

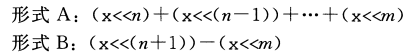
假设加法和减法有同样的性能，那么原则就是当n=m时，选择形式A，当n=m+1时，随便选哪种，而当n>m＋1时，选择形式B。

当 n=m 时，A:x<<n , B:(x<<n+1)-(x<<n) 形式A只需要1个移位,而形式B需要 2个移位和1个减法 ，所以选择A

当n=m+1时，A:(x<<n)+(x<<m)，B:(x<<n+1)-(x<<n)形式A只需要2个移位一个加法，而形式B需要 2个移位和1个减法 ，所以随便选那种

当n>m+1时，就如同上图所展示，很显然选择B

练习题2.42写一个函数 div16，对于整数参数x返回x/16的值。你的函数不能使用除法、模运算、乘法、任何条件语句(if或者?:)、任何比较运算符（例如<、>或= =)或任何循环。你可以假设数据类型int是32位长，使用补码表示，而右移是算术右移。

int book_div16(int x)
{
        /* Compute bias to be either 0 (x >= 0) or 15 (x < 0) */
        int bias = (x >> 31) & 0xF;//右移31位后，32位上面都是符号位的值
        //如果为非负数，符号位为0，bias变量为0
        //如果为负数，符号位为1，bias变量为0xF，即15
        return (x + bias) >> 4;
}

练习题2.43在下面的代码中，我们省略了常数M和N的定义:

#define M /*Mystery number 1 */
#define N /* Mystery number 2*/

int arith(int x, int y)
{
    int result = 0;
    result = x * M + y / N; /*Mand N are mystery numbers. */
    return result;
}

我们以某个M和N的值编译这段代码。编译器用我们讨论过的方法优化乘法和除法。下面是将产生出的机器代码翻译回C语言的结果:

int optarith(int x, int y)
{
    int t = x;
    x <<= 5;
    x -= t;
    if (y < 0)
        y += 7;
    y >>= 3; /* Arithmetic shift */
    return x + y;
}

先看M:
代码等价于x = x 32 -x = x 31.所以M为31.

再看N

7=2\^3-1,最后的右移操作也是右移3位，所以N=8

练习题2.44假设我们在对有符号值使用补码运算的32位机器上运行代码。对于有符号值使用的是算术右移，而对于无符号值使用的是逻辑右移。变量的声明和初始化如下:

int x = foo();
int y = bar();
unsigned ux = x;
unsigned uy = y;

对于下面每个C表达式，1)证明对于所有的x和y值，它都为真(等于1);或者2)给出使得它为假(等于0)的x和y的值:

A. (x > 0)||(x-1 <0)

当x为TMIN时，左边不符合条件，为0；右边负溢出为TMAX，正数不小于0，为0；此时为false

B. (x & 7) != 7 || (x<<29< 0)

左边要求的是x的低3位不能都为1；右边要求第3位为1（先左移29位，所以有原始的低3位和29位个0组成，此时小于0，说明符号位为1，即原始的低3位的最高那个为1）；
低3位分两种情况：
1）除111外的所有情况：左边符合，必返回1，不用管右边。
2）111：左边不符合，但右边符合了，也返回1。
该表达式必为true。

C. (x* x) >= 0

x = 182

182*182-65536=33124-65536=-32412

D. x <0 || -x <=0

当x为0时，右边成立；
当x为[1,TMAX]，右边必成立；
当x为[TMIN+1,-1]，左边成立；
当x为TMIN，左右都成立；
综上，此表达式必为1.

E. x > 0 || -x >= 0

当x为0时，右边成立；
当x为[1,TMAX]，左边成立；
当x为[TMIN+1,-1]，右边成立；
当x为TMIN，左右理论上都不成立（实际上有问题）；

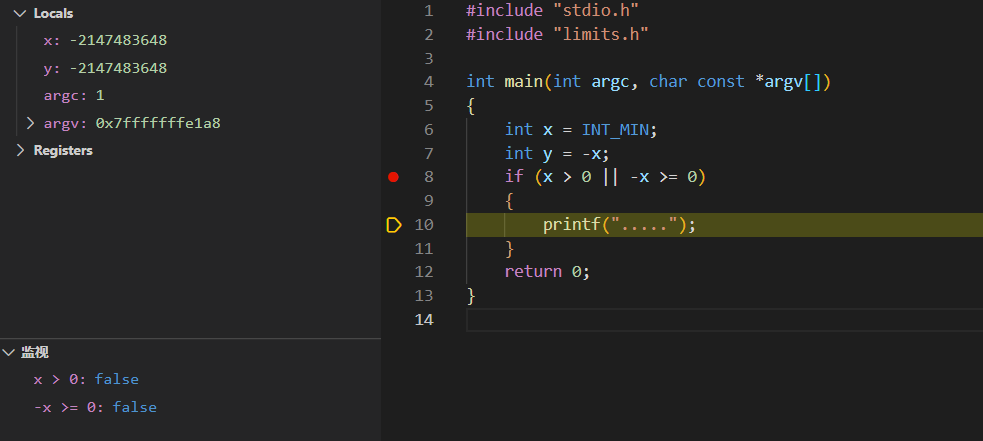
F. x+y == uy+ux

表达式中含有无符号数，所以左边也会转换为无符号数。等价于unsigned(x+y) == uy+ux.
在二进制上，无符号数和有符号数的加法是一样的，故都为真。

G.x*~y + uy*ux=-x

-y = ~y+1,故 ~y=-y-1, 左边= x*(-y-1)+uy*ux = uy*ux - x*y -x, 不管是无符号数还是有符号数，在二进制层面上相乘后截短后的结果都是相同的。故 uy*ux-x*y=0, 故结果都为真

练习题2.45填写下表中的缺失的信息:

小数值	二进制表示	十进制表示
$\frac{1}{8}$	0.001	0.125
$\frac{3}{4}$	0.110	0.75
$\frac{25}{16}$	1.1001	1.5625
$\frac{43}{16}$	10.1011	2.6875
$\frac{9}{8}$	1.001	1.125
$\frac{47}{8}$	101.111	5.875
$\frac{51}{16}$	11.0011	3.1875

练习题2.46

太长了，略。

练习题2.47︰假设一个基于IEEE浮点格式的5位浮点表示，有1个符号位、2个阶码位(k=2)和两个小数位(n=2)。阶码偏置量是$2^{2-1}=1$。

下表中列举了这个5位浮点表示的全部非负取值范围。使用下面的条件，填写表格中的空白项:

$e$:假定阶码字段是一个无符号整数所表示的值。

$E$:偏置之后的阶码值。

$2^E$:阶码的权重。

$f$ :小数值。

$M$:尾数的值。

$2^E×M$:该数(未归约的)小数值。

$V$:该数归约后的小数值。

十进制:该数的十进制表示。

写出$2^E$、f、M、$2^E\times M$和V的值，要么是整数(如果可能的话)，要么是形如$\frac{x}{y}$的小数，这里y是2的幂。标注为“—”的条目不用填。

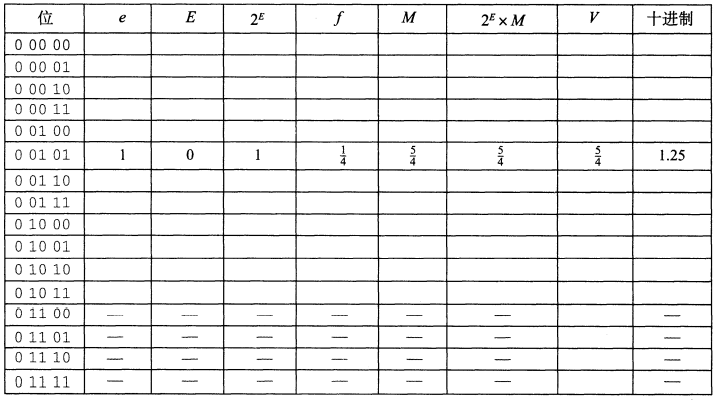
偏置量是$2^{2-1}-1=1$

位	e	$E$	$2^E$	$f$	$M$	$2^E \times M$	$V$	十进制
0 00 00	0	0	1	$\frac{0}{4}$	0	0	0	0.0
0 00 01	0	0	1	$\frac{1}{4}$	$\frac{1}{4}$	$\frac{1}{4}$	$\frac{1}{4}$	0.25
0 00 10	0	0	1	$\frac{2}{4}$	$\frac{2}{4}$	$\frac{2}{4}$	$\frac{1}{2}$	0.5
0 00 11	0	0	1	$\frac{3}{4}$	$\frac{3}{4}$	$\frac{3}{4}$	$\frac{3}{4}$	0.75
0 01 00	1	0	1	$\frac{0}{4}$	$\frac{4}{4}$	$\frac{4}{4}$	$1$	1.0
0 01 01	1	0	1	$\frac{1}{4}$	$\frac{5}{4}$	$\frac{5}{4}$	$\frac{5}{4}$	1.25
0 01 11	1	0	1	$\frac{2}{4}$	$\frac{6}{4}$	$\frac{6}{4}$	$\frac{3}{2}$	1.5
0 10 00	2	1	2	0	$\frac{4}{4}$	$\frac{8}{4}$	$2$	2
0 10 01	2	1	2	$\frac{1}{4}$	$\frac{5}{4}$	$\frac{10}{4}$	$\frac{5}{2}$	2.5
0 10 11	2	1	2	$\frac{2}{4}$	$\frac{6}{4}$	$\frac{12}{4}$	$3$	3
0 11 00	——	——	——	——	——	——	$+\infty$	——
0 11 01	——	——	——	——	——	——	NAN	——
0 11 10	——	——	——	——	——	——	NAN	——
0 11 11	——	——	——	——	——	——	NAN	——

练习题2.48正如在练习题2.6中提到的，整数3 510 593的十六进制表示为0x00359141，而单精度浮点数3510593.0的十六进制表示为0x42564504。推导出这个浮点表示，并解释整数和浮点数表示的位之间的关系。

整数 0x00359141 = 0000 0000 0011 0101 1001 0001 0100 0001

转换成浮点表示时, 先将小数点放在值为 1 的最高有效位的右边, 得到 $1.1 0101 1001 0001 0100 0001_2\times 2^{21} $。

因此尾数值为$1.101011001000101000001_2$，舍弃开头的1，末尾还需要增加两个0 （总共尾数23位），尾数部分为$101 0110 0100 0101 0000 0100$。

对于阶码位数 k=8，$Bias =2^{k-1}-1=2^7-1=127$，指数值 E = 21, E = e-B, 从而 e= 21+127=148,148 = 1001 0100

对于符号位，直接为0

综上，3510593.0 的浮点表示为 0 10010100 10101100100010100000100

而 0x4a564504 的位模式刚好为 010010100101 0110 0100 0101 0000 0100

练习题2.49

A. 对于一种具有n位小数的浮点格式，给出不能准确描述的最小正整数的公式(因为要想准确表示它需要n＋1位小数)。假设阶码字段长度k足够大，可以表示的阶码范围不会限制这个问题。

该练习有助于我们思考什么数不能用浮点数精确表示，因为阶码范围不限制, 故只需考虑小数部分最小能表示的数即可。

小数最多 n 位, 故最小能表示的小数 f 是 n 个 0 后面再加一个 1, 这个小数需要 n+1 个位来表示, 那么尾数 $M = f+1 =1.0000⋯01_2$

即要示的数的二进制表示为：1 后面跟 n 个 0, 再跟一个 1, 值为$2^{n+1}+1$

B. 对于单精度格式(n=23)，这个整数的数字值是多少?

对于单精度格式 n=23, 这个数为 $2^{24}+1=16777217$

练习题2.50根据舍入到偶数规则，说明如何将下列二进制小数值舍入到最接近的二分之一(二进制小数点右边1位)。对每种情况，给出舍入前后的数字值。

A.$10.010_2 = 10.0$

B.$10.011_2 = 10.1$

C.$10.110_2 = 11.0$

D.$11.001_2=11.0$

练习题2.51

练习题2.52考虑下列基于IEEE浮点格式的7位浮点表示。两个格式都没有符号位——它们只能表示非负的数字。

1.格式A

• 有k=3个阶码位。阶码的偏置值是3。
• 有n=4个小数1。

2.格式B

• 有k=4个阶码位。阶码的偏置值是7。
• 有n=3个小数位。

下面给出了一些格式A表示的位模式，你的任务是将它们转换成格式B中最接近的值。如果需要，请使用舍入到偶数的舍入原则。另外，给出由格式A和格式B表示的位模式对应的数字的值。给出整数(例如17)或者小数(例如17/64)。

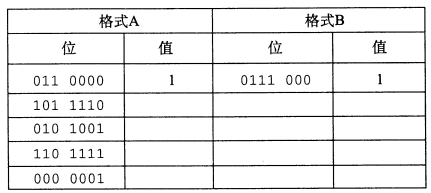
格式A		格式B
位	值	位	值
011 0000	1	0111 000	1
101 1110	$\frac{15}{2}$	1001 111	$\frac{15}{2}$
010 1001	$\frac{25}{32}$	0110 100	$\frac{3}{4}$
110 1111	$\frac{31}{2}$	1010 000	16
000 0001	$\frac{1}{64}$	0001 000	$\frac{1}{64}$

练习题2.53完成下列宏定义，生成双精度值+∞, −∞和 0:

#define POS_INFINITY 1e400
#define NEG_INFINITY (-POS_INFINITY)
#define NEG_ZERO (-1.0/POS_INFINITY)

练习题 2.54 假设变量 x, f, d 类型分别是 int, float, double, 它们除了不是 +∞, −∞ 和 NaN 外,可以是任意值, 对于下面的每个 C 表达式, 证明它们总是真（也就是求值为1）,或者给出一个使其不为真的值（就是求值为0)。

A.x == (int)(double) x
B.x == (int)(float) x
C.d == (double)(float) d
D.f == (float)(double)f
E.f == -(-f)
F.1.0/2 == 1/2.0
G.d*d >= 0.0
H. (f+d)-f == d

float 的最大规格化数是 3.4e38, 小于 1e40, double 的最大规格化数是 1.8e308, 小于 1e309.

A. x == (int)(double) x : int 转换到 double 时能精确转换, 故总为真

B.x == (int)(float) x: int 到 float, 不溢出, 可能舍入, 根据练习题 2.49, 最小不能表示的正数是$2^{23}+1$，此时会舍入到$2^{23}$

C. d == (double)(float) d: double 转换到 float 会溢出,也会舍入, d = 1e40 时右边会是正无穷

D. f == (float)(double)f:　都为真

E. f == -(-f): 都为真, 因为浮点数的正负转换只需转换符号位即可.

F. 1.0/2 == 1/2.0:　都为真, 因为分子和分母在运算前都会先转换成浮点数．

G. d*d >= 0.0：实数乘法符合单调性, 故都为真, 不过可能溢出为 +∞

H. (f+d)-f == d: 当 f+d 溢出时, 不为真, 例如 f=1e20, d=1.0 时, 左边会 0,右边 为 1.0