整数二分

可以划分为满足某种性质与不满足某种性质的两个区间，用二分法可以找到两区间边界的左右两个点。如图中红色和绿色区间，可以通过二分找到这个区间边界。这里需要注意的是利用单调性二分只是其中一种，其他性质其实也可以二分，不过我们掌握单调性进行二分查找就行。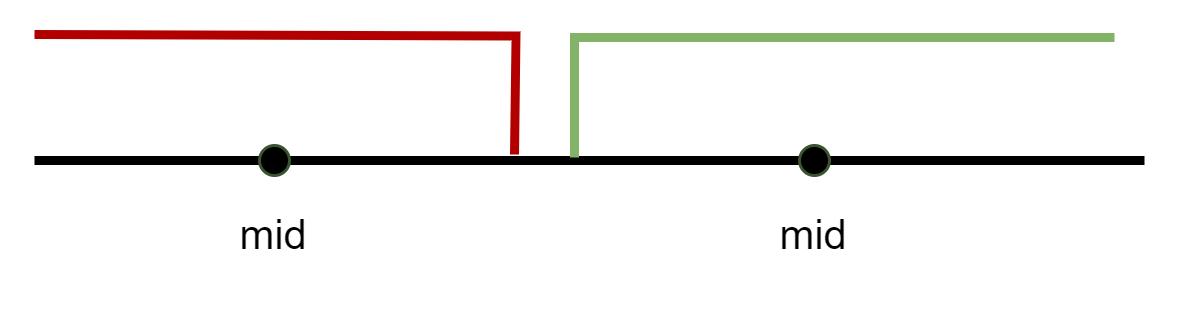

1. 寻找红色区域的边界。
   • mid = (l+r+1)/2
   • 如果mid在红色区域，[l,r]->[mid,r]
   • 如果mid不在红色区域，也就是红色右侧的区域，[l,r]->[l,mid-1]
2. 寻找绿色区域的边界。
   • mid = (l+r)/2
   • 如果mid在绿色区域，[l,r]->[l,mid]
   • 如果mid不在绿色区域，也就是绿色左侧的区域，[l,r]->[mid+1,r]

/**
 * @brief 二分查找
 * 
 */
bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

示例

使用二分查找3的起始位置和终止位置，我可以使用上面的方法进行查找

可以使用bsearch_2查找3的终止位置，条件是x<=3

可以使用bsearch_1查找3的终止位置，条件是x>=3

对应题目

在排序数组中查找元素的第一个和最后一个位置

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        if(nums.empty())return {-1,-1};
        int l = LeftBound(nums,target);

        if(nums[l]!=target){
            return {-1,-1};
        }
        int r = RightBound(nums,target);


        return {l,r};
    }
    // 对应bsearch_1
    int LeftBound(vector<int>& nums, int target)
    {
        int l = 0;
        int r = nums.size() - 1;
        while (l < r)
        {
            int mid = (l + r) >> 1;
            if (nums[mid] >= target)
            {
                r = mid;
            }
            else
            {
                l = mid + 1;
            }
        }
        return l;
    }

    // 对应bsearch_2
    int RightBound(vector<int>& nums, int target)
    {
        int l = 0;
        int r = nums.size() - 1;
        while (l < r)
        {
            int mid = (l + r + 1) >> 1;
            if (nums[mid] <= target)
            {
                l = mid;
            }
            else
            {
                r = mid - 1;
            }
        }
        return l;
    }
};