背包问题
01背包
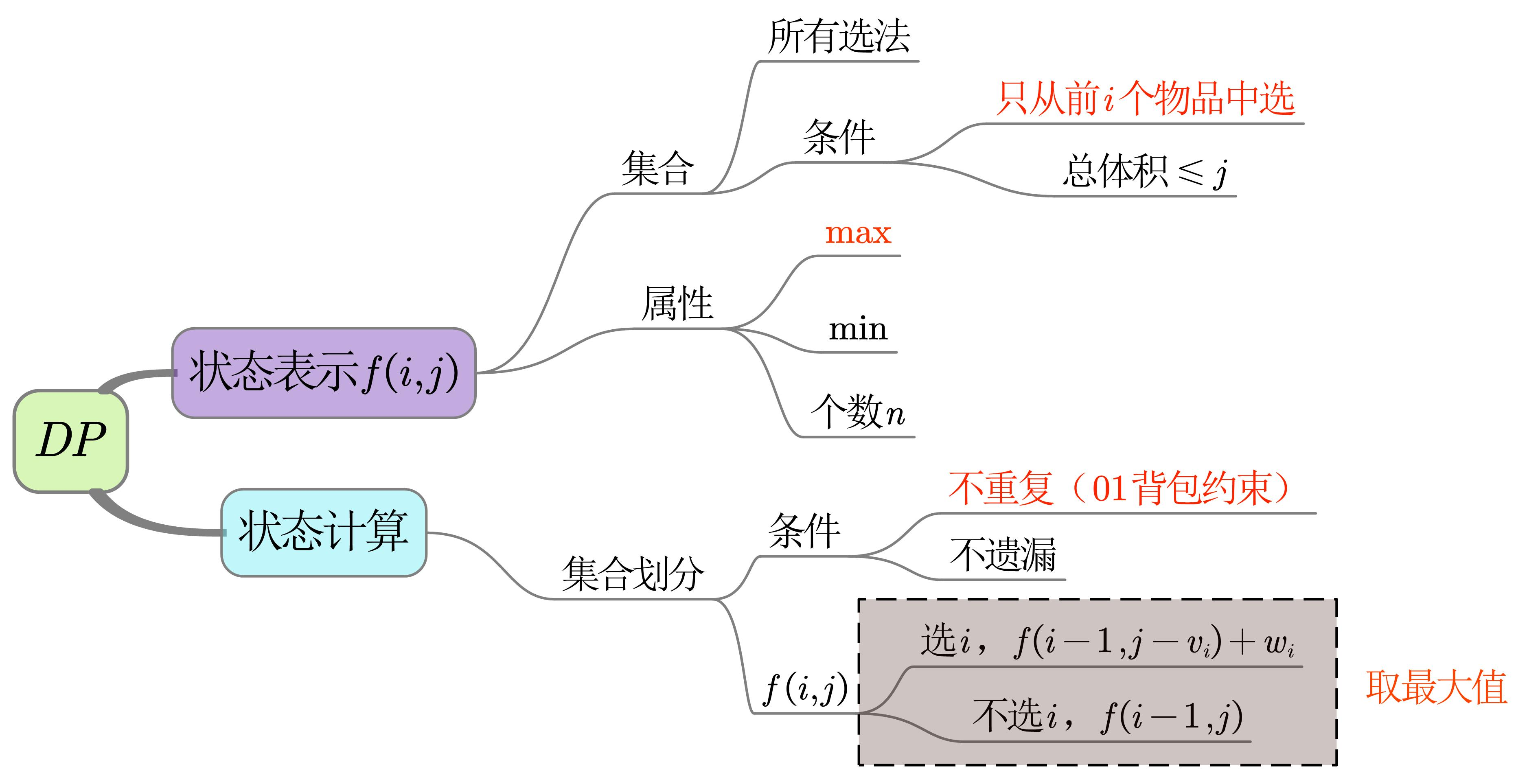
1 | int n; // 物品总数 |
完全背包
所以
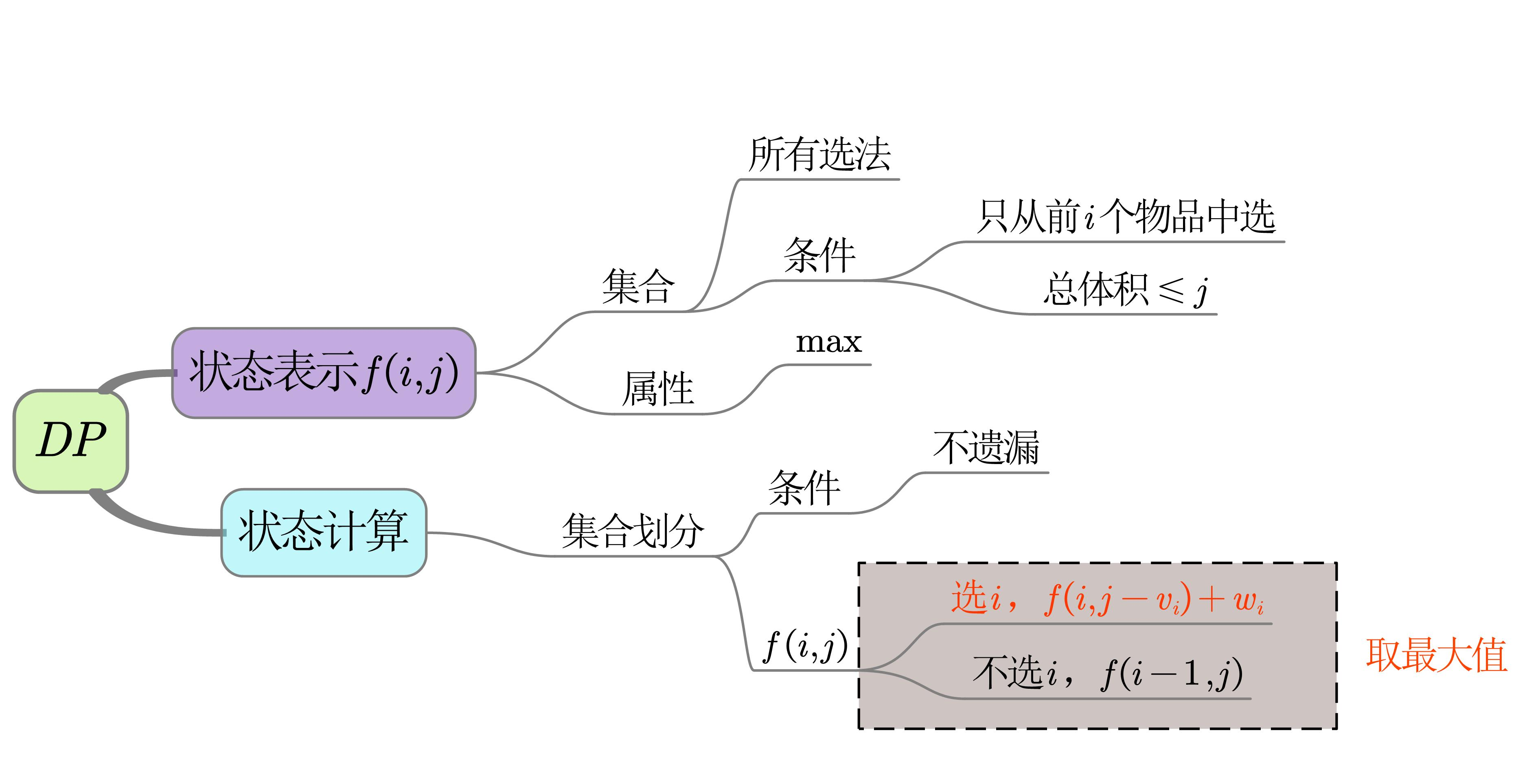
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28int n; // 物品总数
int m; // 背包容量
int W[n+1]; // 重量
int V[m+1]; // 价值
// ---------------二维形式---------------
// 未优化
int f[n+1][m+1]; // f[i][j]表示在考虑前i个物品后,背包容量为j条件下的最大价值
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
for (int k = 0; k * W[i] <= j; k++)
f[i][j] = max(f[i][j], f[i - 1][j - k * W[i]] + k * V[i]);
// 已优化
int f[n+1][m+1]; // f[i][j]表示在考虑前i个物品后,背包容量为j条件下的最大价值
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j)
if(j < W[i]) f[i][j] = f[i-1][j]; // 当前重量装不进,价值等于前i-1个物品
else f[i][j] = max(f[i-1][j], f[i][j-W[i]] + V[i]); // 能装,需判断
cout << f[n][m];
// ---------------一维形式---------------
int f[m+1]; // f[j]表示背包容量为j条件下的最大价值
for(int i = 1; i <= n; ++i)
for(int j = W[i]; j <= m; ++j)
f[j] = max(f[j], f[j - W[i]] + V[i]); // 注意是倒序,否则出现写后读错误
cout << f[m+1]; // 注意是m不是n
完全背包题目
多重背包
多重背包可以转化为01背包然后使用二进制优化进行优化。
朴素做法1
2
3
4
5
6
7
8
9
10
11int n; // 物品总数
int m; // 背包容量
int W[n+1]; // 重量
int V[n+1]; // 价值
// -----------------未优化(完全背包模板)----------------------
int f[n+1][m+!]; // f[i][j]表示在考虑前i个物品后,背包容量为j条件下的最大价值
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
for (int k = 0; k <= S[i] && k * W[i] <= j; k++)
f[i][j] = max(f[i][j], f[i - 1][j - k * W[i]] + k * V[i]);
二进制优化原理
我们用$A_{i,j}$ 代表第 $i$ 种物品拆分出的第 $j$ 个物品。
在朴素的做法中,$\forall j\le ki,A{i,j}$ 均表示相同物品。那么我们效率低的原因主要在于我们进行了大量重复性的工作。举例来说,我们考虑了「同时选 $A{i,1},A{i,2}$」与「同时选 $A{i,2},A{i,3}$」这两个完全等效的情况。这样的重复性工作我们进行了许多次。那么优化拆分方式就成为了解决问题的突破口。
具体地说就是令 $A_{i,j}\left(j\in\left[0,\lfloor \log_2(k_i+1)\rfloor-1\right]\right)$ 分别表示由 $2^{j}$ 个单个物品「捆绑」而成的大物品。特殊地,若 $k_i+1$ 不是 2 的整数次幂,则需要在最后添加一个由 $k_i-2^{\lfloor \log_2(k_i+1)\rfloor-1}$ 个单个物品「捆绑」而成的大物品用于补足。
举几个例子:
6=1+2+3
8=1+2+4+1
18=1+2+4+8+3
31=1+2+4+8+16
显然,通过上述拆分方式,可以表示任意 $\le k_i$ 个物品的等效选择方式。将每种物品按照上述方式拆分后,使用 0-1 背包的方法解决即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29// 读入物品个数时顺便打包
for(int i=0;i<n;i++)
{
// 输入 价值、体积、数量
cin>>a>>b>>s;
int k = 1; // 当前包裹大小
while (k <= s)
{
cnt ++ ; // 实际物品种数
W[cnt] = a * k;
V[cnt] = b * k;
s -= k;
k *= 2; // 倍增包裹大小
}
if (s > 0)
{
// 不足的单独放一个,即C
cnt ++ ;
W[cnt] = a * s;
V[cnt] = b * s;
}
}
n = cnt; // 更新物品种数
// 转换成01背包问题
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= W[i]; j -- )
f[j] = max(f[j], f[j - W[i]] + V[i]);
cout << f[m] << endl;
分组背包
起始就是对每个组进行01背包
$f(i,j)=max{f(i−1,j),f(i−1,j−v(i,k))+w(i,k)}$1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22int n; // 物品总数
int m; // 背包容量
int W[n+1][s+1]; // 重量
int V[n+1][s+1]; // 价值
int S[n+1]; // 各组物品种数
// 读入数据
for (int i = 1; i <= n; i ++ )
{
cin >> S[i];
for (int j = 1; j <= S[i]; j ++ )
cin >> W[i][j] >> V[i][j];
}
// 处理数据
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= 1; j -- )
for (int k = 1; k <= S[i]; k ++ )
if (W[i][k] <= j)
f[j] = max(f[j], f[j - W[i][k]] + V[i][k]);
cout << f[m] << endl;